题目内容
（2016湖南省株洲市）已知，如图一次函数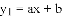
与反比例函数
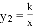的图象如图示，当
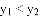时，x的取值范围是（ ）
A. x＜2 B. x＞5 C. 2＜x＜5 D. 0＜x＜2或x＞5
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
天天向上一本好卷系列答案小学生10分钟应用题系列答案题目内容
（2016湖南省株洲市）已知，如图一次函数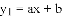与反比例函数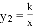的图象如图示，当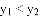时，x的取值范围是（ ）
A. x＜2 B. x＞5 C. 2＜x＜5 D. 0＜x＜2或x＞5
天天向上一本好卷系列答案小学生10分钟应用题系列答案
,AD=2,将长方形纸片沿EF折叠,使点A与点C重合,如果∠BCE=30°,则∠DFE的大小是（ ）
=
B. 
=
C. 
=
D. 
=
