题目内容
 已知直线y1=x,y2=
已知直线y1=x,y2=| 1 |
| 3 |
| 4 |
| 3 |
考点:一次函数的性质
专题:
分析:先判断出y的最大值为直线y2与y3的交点的纵坐标,然后联立两直线解析式求解即可.
解答: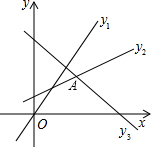 解:根据题意,y的最大值为直线y2与y3的交点的纵坐标,
解:根据题意,y的最大值为直线y2与y3的交点的纵坐标,
联立
,
解得
,
所以,当x=3时,y的值最大,为2.
故答案为:2.
 解:根据题意,y的最大值为直线y2与y3的交点的纵坐标,
解:根据题意,y的最大值为直线y2与y3的交点的纵坐标,联立
|
解得
|
所以,当x=3时,y的值最大,为2.
故答案为:2.
点评:本题考查了一次函数的性质,读懂题目信息,准确识图并判断出y取得最大值时的情况是解题的关键.

练习册系列答案
相关题目
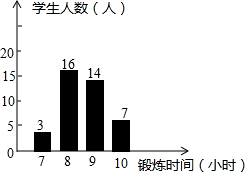 如图所示,是根据某班40名同学一周的体育锻炼情况绘制的条形统计图,那么在作数据分析时,下列说法不正确的是( )
如图所示,是根据某班40名同学一周的体育锻炼情况绘制的条形统计图,那么在作数据分析时,下列说法不正确的是( )| A、极差是3 |
| B、中位数为8 |
| C、众数是8 |
| D、锻炼时间超过8小时的有21人 |