题目内容
(2010•台湾)如图所示,图中甲、乙为两张大小不同的8×8方格纸,其中两正方形PQRS、P’Q’R’S’分别在两方格纸上,且各顶点均在格线的交点上.设两正方形的面积相等,根据图中两正方形的位置,求甲、乙两方格纸的面积比为( )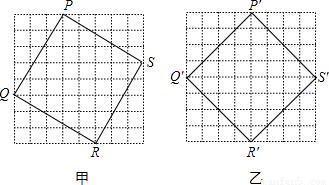
A.4:5
B.9:10
C.15:16
D.16:17
【答案】分析:面积相等说明边长相等,设甲方格纸每一小格长度为a,乙方格纸每一小格长度为b,则(3a)2+(5a)2=(4b)2+(4b)2可得出a和b的关系,也可求的面积的关系.
解答:解:设甲方格纸每一小格长度为a,乙方格纸每一小格长度为b,
则(3a)2+(5a)2=(4b)2+(4b)
∴a2:b2=16:17
即为面积之比.
故选D.
点评:考查正方形面积于边长的关系,此题关键在于设出甲方格纸每一小格长度为a,乙方格纸每一小格长度为b.本题还可以根据正方形在方格纸上占面积的比例进行求解.
解答:解:设甲方格纸每一小格长度为a,乙方格纸每一小格长度为b,
则(3a)2+(5a)2=(4b)2+(4b)
∴a2:b2=16:17
即为面积之比.
故选D.
点评:考查正方形面积于边长的关系,此题关键在于设出甲方格纸每一小格长度为a,乙方格纸每一小格长度为b.本题还可以根据正方形在方格纸上占面积的比例进行求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目