题目内容
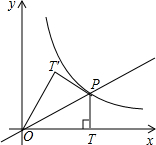 (2011•泉州质检)如图,点P(m,1)是双曲线y=
(2011•泉州质检)如图,点P(m,1)是双曲线y=
| ||
| x |
分析:先把点P(m,1)代入双曲线y=
求出m的值,再根据锐角三角函数的定义求出∠TOP的度数,根据翻折变换的性质皆可得出∠T′OT的度数.
| ||
| x |
解答:解:∵点P(m,1)是双曲线y=
上的一点,
∴1=
,解得m=
,
∴tan∠TOP=
,
∵点P在是第一象限的点,
∴∠TOP=30°,
∵△OT′P是△OTP翻折而成,
∴∠TOP=∠T′OP=30°,
∴∠T′OT=∠TOP+∠T′OP=60°.
故选D.
| ||
| x |
∴1=
| ||
| m |
| 3 |
∴tan∠TOP=
| ||
| 3 |
∵点P在是第一象限的点,
∴∠TOP=30°,
∵△OT′P是△OTP翻折而成,
∴∠TOP=∠T′OP=30°,
∴∠T′OT=∠TOP+∠T′OP=60°.
故选D.
点评:本题考查的是反比例函数图象上点的坐标特点及特殊角的三角函数值、图形翻折变换的性质,熟知以上知识是解答此题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
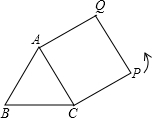 将正方形ACPQ沿逆时针方向旋转α,使AQ与AB重合,则:
将正方形ACPQ沿逆时针方向旋转α,使AQ与AB重合,则: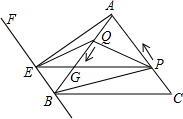 用“>、<、=、≥、≤”符号表示);
用“>、<、=、≥、≤”符号表示);