题目内容
Rt△ABO的顶点A是双曲线y=| k |
| x |
| 3 |
| 2 |
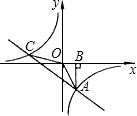 如图.
如图.(1)求二函数解析式;
(2)求直线和双曲线的交点坐标;
(3)S△AOC.
分析:(1)由S△ABO=
,根据反比例函数的系数k几何意义,即可求出k的值;
(2)将两函数解析式组成方程组,求出方程组的解即为交点坐标;
(3)求出直线AC和x轴的交点坐标,结合A、C的坐标,利用三角形的面积公式即可求出S△AOC.
| 3 |
| 2 |
(2)将两函数解析式组成方程组,求出方程组的解即为交点坐标;
(3)求出直线AC和x轴的交点坐标,结合A、C的坐标,利用三角形的面积公式即可求出S△AOC.
解答:解:(1)∵S△ABO=
,
∴|k|=2×
=3,
由于反比例函数的图象位于二、四象限,
∴k=-3,
∴反比例函数解析式为y=-
.
一次函数解析式为y=-x-3+1,
即y=-x-2.
(2)将反比例函数解析式为y=-
和一次函数解析式为y=-x-2,组成方程组得,
,
解得
,
.
所以直线和双曲线的交点坐标为A(1,-3),C(-3,1).
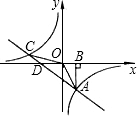
(3)如图,令y=0,则有-x-2=0,
解得x=-2,故D点坐标为(-2,0).
∵D(-2,0),C(-3,1),
∴S△AOC=S△DOC+S△AOD
=
×2×1+
×2×3
=1+3=4.
| 3 |
| 2 |
∴|k|=2×
| 3 |
| 2 |
由于反比例函数的图象位于二、四象限,
∴k=-3,
∴反比例函数解析式为y=-
| 3 |
| x |
一次函数解析式为y=-x-3+1,
即y=-x-2.
(2)将反比例函数解析式为y=-
| 3 |
| x |
|
解得
|
|
所以直线和双曲线的交点坐标为A(1,-3),C(-3,1).

(3)如图,令y=0,则有-x-2=0,
解得x=-2,故D点坐标为(-2,0).
∵D(-2,0),C(-3,1),
∴S△AOC=S△DOC+S△AOD
=
| 1 |
| 2 |
| 1 |
| 2 |
=1+3=4.
点评:此题考查了反比例函数的几何意义、反比例函数和一次函数的交点坐标及和图象有关的三角形的面积,求出交点坐标是解题关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
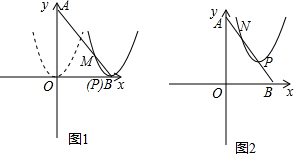
 S△ABO=
S△ABO= 10、如图,平面直角坐标系内Rt△ABO的顶点A坐标为(3,1),将△ABO绕O点逆时针旋转90°后,顶点A的坐标为( )
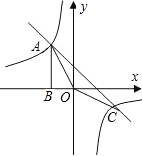
10、如图,平面直角坐标系内Rt△ABO的顶点A坐标为(3,1),将△ABO绕O点逆时针旋转90°后,顶点A的坐标为( ) 如图,Rt△ABO的顶点A是反比例函数y=
如图,Rt△ABO的顶点A是反比例函数y=