题目内容
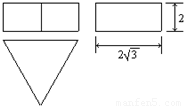
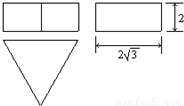
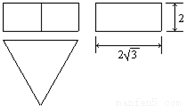
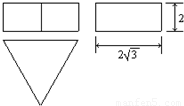
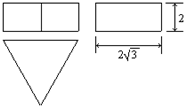 如图为一机器零件的三视图.
如图为一机器零件的三视图.(1)请写出符合这个机器零件形状的几何体的名称;
(2)若俯视图中三角形为正三角形,那么请根据图中所标的尺寸,计算这个几何体的表面积(单位:cm2)
分析:(1)有2个视图的轮廓是长方形,那么这个几何体为棱柱,另一个视图是三角形,那么该几何体为三棱柱;
(2)根据正三角形一边上的高可得正三角形的边长,表面积=侧面积+2个底面积=底面周长×高+2个底面积.
(2)根据正三角形一边上的高可得正三角形的边长,表面积=侧面积+2个底面积=底面周长×高+2个底面积.
解答: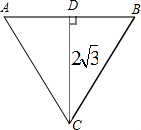 解:(1)符合这个零件的几何体是直三棱柱;
解:(1)符合这个零件的几何体是直三棱柱;
(2)∵△ABC是正三角形,
又∵CD⊥AB,CD=2
,
∴AC=
=4,
∴S表面积=4×2×3+2×4×
×2
,
=24+8
(cm2).
 解:(1)符合这个零件的几何体是直三棱柱;
解:(1)符合这个零件的几何体是直三棱柱;(2)∵△ABC是正三角形,
又∵CD⊥AB,CD=2
| 3 |
∴AC=
| CD |
| sin60° |
∴S表面积=4×2×3+2×4×
| 1 |
| 2 |
| 3 |
=24+8
| 3 |
点评:考查由三视图判断几何体及几何体表面积的计算;得到几何体的形状是解决本题的突破点;得到底面的边长是解决本题的易错点.

练习册系列答案
相关题目