题目内容
【题目】如图,已知![]() 的顶点A和AB边的中点C都在双曲线
的顶点A和AB边的中点C都在双曲线![]() 的一个分支上,点B在x轴上,则
的一个分支上,点B在x轴上,则![]() 的面积为
的面积为

A.3B.4C.6D.8
【答案】C
【解析】
,结合图形可得:S△ABO=S△AOM+S△AMB,分别求解出S△AOM、S△AMB的值,过点A、C分别作AM⊥OB于M、CD⊥OB于D,设点A坐标为(x,y),设B的坐标为(a,0),已知点C是线段AB的中点, 由点A位于反比例函数的图象上可得:xy=4,即S△AOM=2,接下来,根据点C的坐标为(![]() ),同理可解得S△CDO的面积,接下来,由S△AMB=
),同理可解得S△CDO的面积,接下来,由S△AMB=![]() ×AM×BM,MB=|ax|,AM=y,可解得S△AMB,即可确定△ABO的面积.
×AM×BM,MB=|ax|,AM=y,可解得S△AMB,即可确定△ABO的面积.
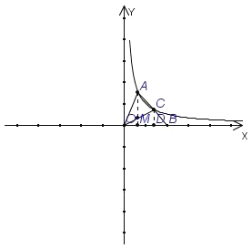
解:过点A、C分别作AM⊥OB于M、CD⊥OB于D,设点A坐标为(x,y)
∵ 顶点A在双曲线y=![]() (x>0)图象上
(x>0)图象上
∴ xy=4
∵ AM⊥OB
∴ S△AMO=![]() ×AM×OM=
×AM×OM=![]() ×xy,S△AMB=
×xy,S△AMB=![]() ×AM×BM (三角形的面积等于一边与此边上高的乘积的一半)
×AM×BM (三角形的面积等于一边与此边上高的乘积的一半)
∵ S△AMO=![]() ×xy, xy=4
×xy, xy=4
∴ S△AMO=2
设B的坐标为(a,0)
∵ 点C是线段AB的中点 点A、B坐标为(x,y)、(a,0)
∴ 点C坐标为(![]() )
)
∵ CD⊥OB 点C坐标为(![]() )
)
∴ S△CDO=![]() ×CD×OD=
×CD×OD=![]() ×(
×(![]() )×(
)×(![]() )=2 (三角形的面积等于一边与此边上高的乘积的一半)
)=2 (三角形的面积等于一边与此边上高的乘积的一半)
故ay=2
∵ S△AMB=![]() ×AM×BM,MB=|ax| ,AM=y
×AM×BM,MB=|ax| ,AM=y
∴ S△AMB=![]() span>×|ax|×y=4
span>×|ax|×y=4
∵ S△ABO=S△AOM+S△AMB,S△AOM=2,S△AMB=4
∴ S△ABO=6
即△ABO的面积是6,答案选C.

练习册系列答案
相关题目