题目内容
【题目】如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作分、FG∥CD,交AE于点G连接DG. 
(1)求证:四边形DEFG为菱形;
(2)若CD=8,CF=4,求 ![]() 的值.
的值.
【答案】
(1)证明:由折叠的性质可知:DG=FG,ED=EF,∠1=∠2,
∵FG∥CD,
∴∠2=∠3,
∴FG=FE,
∴DG=GF=EF=DE,
∴四边形DEFG为菱形
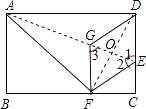
(2)解:设DE=x,根据折叠的性质,EF=DE=x,EC=8﹣x,
在Rt△EFC中,FC2+EC2=EF2,
即42+(8﹣x)2=x2,
解得:x=5,CE=8﹣x=3,
∴ ![]() =
= ![]()
【解析】(1)根据折叠的性质,易知DG=FG,ED=EF,∠1=∠2,由FG∥CD,可得∠1=∠3,易证FG=FE,故由四边相等证明四边形DEFG为菱形;(2)在Rt△EFC中,用勾股定理列方程即可CD、CE,从而求出 ![]() 的值.
的值.
【考点精析】关于本题考查的勾股定理的概念和矩形的性质,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;矩形的四个角都是直角,矩形的对角线相等才能得出正确答案.

练习册系列答案
相关题目
【题目】用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素C含量及购买这两种原料的价格如下表:
甲种原料 | 乙种原料 | |
维生素C含量(单位千克) | 600 | 100 |
原料价格(元千克) | 8 | 4 |
现配制这种饮料10kg,要求至少含有4200单位的维生素C,若所需甲种原料的质量为x kg,则x应满足的不等式为( )
A.600x+100(10﹣x)≥4200
B.8x+4(100﹣x)≤4200
C.600x+100(10﹣x)≤4200
D.8x+4(100﹣x)≥4200