جâؤ؟ؤعبف
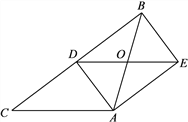
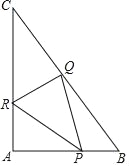
،¾جâؤ؟،؟بçح¼£¬ض±½ا،÷ABCضذ£¬،دAخھض±½ا£¬AB£½6£¬AC£½8£®µمP،¢Q،¢R·ض±ًشعAB،¢BC،¢CA±كةدح¬ت±؟ھت¼×÷شبثظشث¶¯£¬2أë؛َب¸ِµمح¬ت±ح£ض¹شث¶¯£¬µمPسةµمA³ِ·¢زشأ؟أë3¸ِµ¥خ»µؤثظ¶بدٍµمBشث¶¯£¬µمQسةµمB³ِ·¢زشأ؟أë5¸ِµ¥خ»µؤثظ¶بدٍµمCشث¶¯£¬µمRسةµمC³ِ·¢زشأ؟أë4¸ِµ¥خ»µؤثظ¶بدٍµمAشث¶¯£¬سأt£¨أ룩£¨0،ـt،ـ2£©±يت¾شث¶¯ت±¼ن£¬شعشث¶¯¹³جضذ£؛
£¨1£©µ±tخھ؛خضµت±£¬،÷APRµؤأو»خھ4£»
£¨2£©اَ³ِ،÷CRQµؤ×î´َأو»£»
£¨3£©تا·ٌ´وشعt£¬ت¹،دPQR£½90،م£؟بô´وشع£¬اëاَ³ِtµؤضµ£»بô²»´وشع£¬اëثµأ÷ہيسة£®
،¾´ً°¸،؟£¨1£©![]() »ٍ
»ٍ![]() أ룻£¨2£©µ±t£½1ت±£¬S،÷CQR×î´َ£½6£»£¨3£©tµؤضµخھ1أë»ٍ
أ룻£¨2£©µ±t£½1ت±£¬S،÷CQR×î´َ£½6£»£¨3£©tµؤضµخھ1أë»ٍ![]() أ룮
أ룮
،¾½âخِ،؟
£¨1£©سةشث¶¯µأ³ِAP£½3t£¬AR£½8©پ4t£¬×î؛َسأب½اذخأو»¹«ت½½¨ء¢·½³جاَ½â¼´؟ةµأ³ِ½لآغ£»
£¨2£©دب¹¹شى³ِض±½اب½اذخ±يت¾³ِQD£¬×î؛َسأب½اذخأو»¹«ت½¼´؟ةµأ³ِ½لآغ£»
£¨3£©دبإذ¶د³ِ،÷BFP،×،÷BAC£¬µأ³ِFP£½![]() £¨6©پ3t£©£¬BF£½
£¨6©پ3t£©£¬BF£½![]() £¨6©پ3t£©£¬½ّ¶ّFQ£½BQ©پBF£½5t©پ
£¨6©پ3t£©£¬½ّ¶ّFQ£½BQ©پBF£½5t©پ![]() £¨6©پ3t£©£½
£¨6©پ3t£©£½![]()
ح¬ہي£؛EQ£½![]() £¬RE£½
£¬RE£½![]() £¬شظإذ¶د³ِ،÷REQ،×،÷QFP£®µأ³ِ
£¬شظإذ¶د³ِ،÷REQ،×،÷QFP£®µأ³ِ![]() £¬سأRE،ءFP£½QF،ءEQ½¨ء¢·½³جاَ½â¼´؟ةµأ³ِ½لآغ£®
£¬سأRE،ءFP£½QF،ءEQ½¨ء¢·½³جاَ½â¼´؟ةµأ³ِ½لآغ£®
£¨1£©سةشث¶¯ضھ£¬AP£½3t£¬CR£½4t£¬
،àAR£½8©پ4t£¬
،àS،÷APR£½![]() APAR£½
APAR£½![]() ،ء3t،ء£¨8©پ4t£©£½12t©پ6t2£½4£¬
،ء3t،ء£¨8©پ4t£©£½12t©پ6t2£½4£¬
½âµأt£½![]() »ٍt£½
»ٍt£½![]()
،൱tخھ![]() »ٍ
»ٍ![]() أëت±£¬،÷APRµؤأو»خھ4£»
أëت±£¬،÷APRµؤأو»خھ4£»
£¨2£©بçح¼1£¬¹µمQ×÷QD،حACسعD£¬
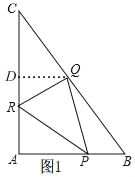
شعRt،÷ABCضذ£¬AB£½6£¬AC£½8£¬¸ù¾ف¹´¹ة¶¨ہيµأ£¬BC£½10£¬
،àsinC£½![]() £¬
£¬
سةشث¶¯ضھ£¬BQ£½5t£¬CR£½4t£¬
،àCQ£½BC©پBQ£½10©پ5t£¬
،àشعRt،÷CDQضذ£¬QD£½CQsinC£½![]() £¨10©پ5t£©£½6©پ3t£¬
£¨10©پ5t£©£½6©پ3t£¬
،àS،÷CQR£½![]() CRQD£½
CRQD£½![]() ،ء4t،ء£¨6©پ3t£©£½12t©پ6t2£½©پ6£¨t©پ1£©2+6£¬
،ء4t،ء£¨6©پ3t£©£½12t©پ6t2£½©پ6£¨t©پ1£©2+6£¬
،ك0،ـt،ـ2£¬
،൱t£½1ت±£¬S،÷CQR×î´َ£½6£»
£¨3£©´وشع£¬بçح¼2£¬¹µمR×÷RE،حBCسعE£¬¹µمP×÷PF،حBCسعF£¬
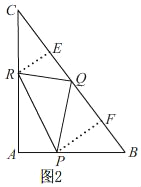
سةجâزâضھ£¬CR£½4t£¬BQ£½5t£¬AP£½3t£¬
،àBP£½6©پ3t£¬
،ك،دBFP£½،دA£½90،م£¬،دB£½،دB£¬
،à،÷BFP،×،÷BAC£¬
،à![]() £¬
£¬
،à![]() £¬
£¬
،àFP£½![]() £¨6©پ3t£©£¬BF£½
£¨6©پ3t£©£¬BF£½![]() £¨6©پ3t£©£¬
£¨6©پ3t£©£¬
،àFQ£½BQ©پBF£½5t©پ![]() £¨6©پ3t£©£½
£¨6©پ3t£©£½![]()
ح¬ہي£؛EQ£½![]() £¬RE£½
£¬RE£½![]() £¬
£¬
،ك،دREQ£½،دQFP£½90،م£¬
،à،دERQ+،دEQR£½90،م£¬
،ك،دPQR£½90،م£¬
،à،دEQR+،دPQF£½90،م£¬
،à،دERQ£½،دPQF£¬
،à،÷REQ،×،÷QFP£®
،à![]() £¬
£¬
،àRE،ءFP£½QF،ءEQ£¬
،à![]() ،ء
،ء![]() £¨6©پ3t£©£½
£¨6©پ3t£©£½![]() ،ء
،ء![]() £¬
£¬
½âµأ£¬t£½1»ٍt£½![]()
،àtµؤضµخھ1أë»ٍ![]() أ룮
أ룮