题目内容
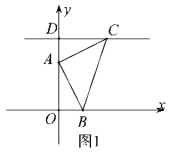
【题目】如图1,平面直角坐标系中,![]() ,
,![]() ,
,![]() ,
,![]() 轴于点
轴于点![]() .
.
(1)![]() ;
;
(2)连接![]() ,判断
,判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)如图2,已知![]() ,
,![]() ,若
,若![]() 是等腰直角三角形,且
是等腰直角三角形,且![]() ,则点
,则点![]() 坐标为 .
坐标为 .

【答案】(1)见解析;(2)![]() 为等腰直角三角形,见解析;(3)
为等腰直角三角形,见解析;(3)![]() 或
或![]()
【解析】
(1)根据点的坐标分别求出OD、CD,得到AD=OB,利用SAS定理证明△AOB≌△CDA;
(2)根据全等三角形的性质得到∠ABO=∠CAD,AC=AB,根据同角的余角相等得到∠BAC=90°,根据等腰直角三角形的定义解答;
(3)根据题意画出点M和点M′,过点P作x轴的平行线GH,作MG⊥GH于G,QH⊥GH于H,证明△GMP≌△HPQ,根据全等三角形的性质得到GM=PH=3,GP=HQ=2,得到点M坐标为(1,1),同理求出点M′坐标.
(1)∵C(2,3),![]() 轴于点
轴于点![]() ,
,
∴D(0,3)
∴OD=3,CD=2,
∵A(0,2),B(1,0),
∴OA=2,OB=1,
∴AD=1,
∴AD=OB,
在△AOB和△CDA中,
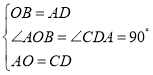 ,
,
∴△AOB≌△CDA(SAS);
(2)△ABC是等腰直角三角形,
理由如下:∵△AOB≌△CDA,
∴∠ABO=∠CAD,AC=AB,
∵∠ABO+∠BAO=90°,
∴∠CAD+∠BAO=90°,
∴∠BAC=90°,又AC=AB,
∴△ABC是等腰直角三角形;
(3)如图2,过点P作x轴的平行线GH,作MG⊥GH于G,QH⊥GH于H,
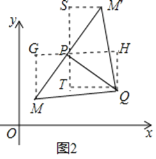
∵P(3,4),Q(6,2),
∴PH=3,QH=2,
∵△MPQ为等腰直角三角形,
∴∠MPQ=90°,PM=PQ,
∴∠MPG+∠HPQ=90°,
∵∠MPG+∠PMG=90°,
∴∠GMP=∠HPQ,
在△GMP和△HPQ中,
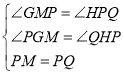 ,
,
∴△GMP≌△HPQ(AAS)
∴GM=PH=3,GP=HQ=2,
∴点M坐标为(1,1),
过点P作y轴的平行线ST,作M′S⊥ST于S,QT⊥ST于T,
同理可得,△M′ST≌△PTQ,
∴M′S=PT=2,SP=TQ=3,
∴点M′坐标为(5,7),
故答案为:(1,1)或(5,7).