题目内容
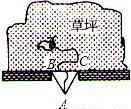
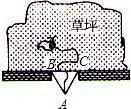 如图所示,一只羊用一条长12米的绳子拴住,绳子的另一头被绑在一堵墙的大门外的点A处,大门的边缘底下B,C两点恰好与点A构成了等边三角形ABC的顶点,如果墙的那一边是一片足够大的草场,△ABC的边长为6米,那么这只羊最多可以吃到多少平方米的草(精确到0.1平方米)?
如图所示,一只羊用一条长12米的绳子拴住,绳子的另一头被绑在一堵墙的大门外的点A处,大门的边缘底下B,C两点恰好与点A构成了等边三角形ABC的顶点,如果墙的那一边是一片足够大的草场,△ABC的边长为6米,那么这只羊最多可以吃到多少平方米的草(精确到0.1平方米)?
分析:首先要分析羊可以吃到的草的最大面积由三部分组成:
第一部分:以点A为圆心,12米为半径,圆心角为60°的扇形的面积减去三角形ABC的面积;
第二部分:以点B为圆心,6米为半径,圆心角为60°的扇形面积;
第三部分与第二部分相等.
第一部分:以点A为圆心,12米为半径,圆心角为60°的扇形的面积减去三角形ABC的面积;
第二部分:以点B为圆心,6米为半径,圆心角为60°的扇形面积;
第三部分与第二部分相等.
解答:解:羊可以吃到的草的最大面积由三部分组成:
第一部分:以点A为圆心,12米为半径.圆心角为60°的扇形的面积减去三角形ABC的面积;
第二部分:以点B为圆心,6米为半径,圆心角为60°的扇形面积;
第三部分与第二部分相等.
因此,羊可以吃到的草的面积是:
-
•62sin60°+2×
≈97.5(平方米).
第一部分:以点A为圆心,12米为半径.圆心角为60°的扇形的面积减去三角形ABC的面积;
第二部分:以点B为圆心,6米为半径,圆心角为60°的扇形面积;
第三部分与第二部分相等.
因此,羊可以吃到的草的面积是:
| 60π•122 |
| 360 |
| 1 |
| 2 |
| 60π•62 |
| 360 |
点评:本题的关键是仔细观察图形分析羊可以吃到的草的最大面积由三部分组成,然后再利用扇形面积公式进行计算.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
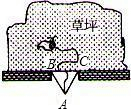 如图所示,一只羊用一条长12米的绳子拴住,绳子的另一头被绑在一堵墙的大门外的点A处,大门的边缘底下B,C两点恰好与点A构成了等边三角形ABC的顶点,如果墙的那一边是一片足够大的草场,△ABC的边长为6米,那么这只羊最多可以吃到多少平方米的草(精确到0.1平方米)?
如图所示,一只羊用一条长12米的绳子拴住,绳子的另一头被绑在一堵墙的大门外的点A处,大门的边缘底下B,C两点恰好与点A构成了等边三角形ABC的顶点,如果墙的那一边是一片足够大的草场,△ABC的边长为6米,那么这只羊最多可以吃到多少平方米的草(精确到0.1平方米)?