题目内容
平面直角坐标系中有六个点A(1,5),B(-3,-| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
| 2 |
分析:根据反比例函数中k=xy的特点分别求出各点所在反比例函数的解析式中k的值,找出不同的值即可.
解答:解:A点所在的反比例函数中k=1×5=5;
B、点所在的反比例函数中k=(-3)×(-
)=5;
C、点所在的反比例函数中k=(-5)×(-1)=5;
D、点所在的反比例函数中k=(-2)×
=-5;
E、点所在的反比例函数中k=3×
=5;
F、点所在的反比例函数中k=
×2=5.
故只有D点与其它点不在这个反比例函数图象上.
B、点所在的反比例函数中k=(-3)×(-
| 5 |
| 3 |
C、点所在的反比例函数中k=(-5)×(-1)=5;
D、点所在的反比例函数中k=(-2)×
| 5 |
| 2 |
E、点所在的反比例函数中k=3×
| 5 |
| 3 |
F、点所在的反比例函数中k=
| 5 |
| 2 |
故只有D点与其它点不在这个反比例函数图象上.
点评:此题比较简单,解答此题的关键是熟知反比例函数中,若各点在同一图象上,则k值相同,即各点的横、纵坐标之积的值不变.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
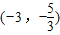 ,C(-5,-1),D
,C(-5,-1),D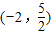 ,E
,E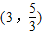 ,F
,F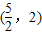 ,其中有五个点在同一反比例函数图象上,则不在这个反比例函数图象上的点是 .
,其中有五个点在同一反比例函数图象上,则不在这个反比例函数图象上的点是 .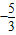 ),C(-5,-1),D(-2,
),C(-5,-1),D(-2, ),E(3,
),E(3, ),F(
),F( ,2).其中有五个点在同一反比例函数图象上,不在这个反比例函数图象上的点是( )
,2).其中有五个点在同一反比例函数图象上,不在这个反比例函数图象上的点是( )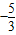 ),C(-5,-1),D(-2,
),C(-5,-1),D(-2, ),E(3,
),E(3, ),F(
),F( ,2).其中有五个点在同一反比例函数图象上,不在这个反比例函数图象上的点是( )
,2).其中有五个点在同一反比例函数图象上,不在这个反比例函数图象上的点是( )