题目内容
请阅读材料:
①一般地,n个相同的因数a相乘:记为an,如23=8,此时,指数3叫做以2为底8的对数,记为log28log=3(即log28=3).
②一般地,若an=b(a>0且a≠1,b>0),则指数n叫做以a为底b的对数,记为logab(即logab=n),如34=81,则指数4叫做以3为底81的对数,记为log381(即log381=4).
(1)计算下列各对数的值:
log24=
(2)观察(1)题中的三数4、16、64之间存在的关系式是
(3)由(2)题的结果,你能归纳出一个一般性的结论吗?
logaM+logaN=
(4)请你运用幂的运算法则am•an=am+n以及上述中对数的定义证明(3)中你所归纳的结论.
①一般地,n个相同的因数a相乘:记为an,如23=8,此时,指数3叫做以2为底8的对数,记为log28log=3(即log28=3).
②一般地,若an=b(a>0且a≠1,b>0),则指数n叫做以a为底b的对数,记为logab(即logab=n),如34=81,则指数4叫做以3为底81的对数,记为log381(即log381=4).
(1)计算下列各对数的值:
log24=
2
2
; log216=4
4
; log264=6
6
.(2)观察(1)题中的三数4、16、64之间存在的关系式是
4×16=64
4×16=64
,那么log24、log216、log264存在的关系式是log24+log216=log264
log24+log216=log264
.(3)由(2)题的结果,你能归纳出一个一般性的结论吗?
logaM+logaN=
logaMN
logaMN
(a>0且a≠1,M>0,N>0)(4)请你运用幂的运算法则am•an=am+n以及上述中对数的定义证明(3)中你所归纳的结论.
分析:(1)根据对数的定义求解;
(2)认真观察,不难找到规律:4×16=64,log24+log216=log264;
(3)有特殊到一般,得出结论:logaM+logaN=loga(MN);
(4)首先可设logaM=b1,logaN=b2,再根据幂的运算法则:an•am=an+m以及对数的含义证明结论.
(2)认真观察,不难找到规律:4×16=64,log24+log216=log264;
(3)有特殊到一般,得出结论:logaM+logaN=loga(MN);
(4)首先可设logaM=b1,logaN=b2,再根据幂的运算法则:an•am=an+m以及对数的含义证明结论.
解答:解:(1)∵22=4,∴log24=2,
∵24=16,∴log216=4,
∵26=64,∴log264=6;
(2)4×16=64,log24+log216=log264;
(3)logaM+logaN=loga(MN);
(4)证明:设logaM=x,logaN=y,
则ax=M,ay=N,
∴MN=ax•ay=ax+y,
∴x+y=loga(MN)即logaM+logaN=loga(MN).
故答案为:2,4,6.
∵24=16,∴log216=4,
∵26=64,∴log264=6;
(2)4×16=64,log24+log216=log264;
(3)logaM+logaN=loga(MN);
(4)证明:设logaM=x,logaN=y,
则ax=M,ay=N,
∴MN=ax•ay=ax+y,
∴x+y=loga(MN)即logaM+logaN=loga(MN).
故答案为:2,4,6.
点评:此题主要考查了同底数幂的乘法应用,本题是开放性的题目,难度较大.借考查对数,实际考查学生对指数的理解、掌握的程度;要求学生不但能灵活、准确的应用其运算法则,还要会类比、归纳,推测出对数应有的性质.

练习册系列答案
相关题目
 记为
记为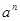 ,如2·2·2=23=8,此时,3叫做以2为底8的对数,记为
,如2·2·2=23=8,此时,3叫做以2为底8的对数,记为 (即
(即 =
= =3).②一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为
=3).②一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为 (即
(即 =n),如34=81,则4叫做以3为底81的对数,记为
=n),如34=81,则4叫做以3为底81的对数,记为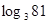 (即
(即 =4).
=4). 4= _____________________________ ;
4= _____________________________ ; M+
M+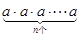 记为
记为 ,如2·2·2=23=8,此时,3叫做以2为底8的对数,记为
,如2·2·2=23=8,此时,3叫做以2为底8的对数,记为 (即
(即 =
= =3).②一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为
=3).②一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为 (即
(即 =n),如34=81,则4叫做以3为底81的对数,记为
=n),如34=81,则4叫做以3为底81的对数,记为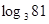 (即
(即 =4).
=4). 4= _____________________________ ;
4= _____________________________ ; M+
M+ 记为
记为 ,如2·2·2=23=8,此时,3叫做以2为底8的对数,记为
,如2·2·2=23=8,此时,3叫做以2为底8的对数,记为 (即
(即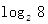 =
= =3).②一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为
=3).②一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为 (即
(即 =n),如34=81,则4叫做以3为底81的对数,记为
=n),如34=81,则4叫做以3为底81的对数,记为 (即
(即 =4).
=4). 4= _____________________________ ;
4= _____________________________ ; M+
M+