Question

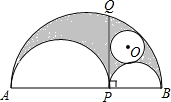如图所示：AP、PB、AB分别是三个半圆的直径，PQ⊥AB，面积为9π的圆O与两个半圆及PQ都相切，而阴影部分的面积是39π，则AB的长是

 

．

Answer 1

分析：设最大圆的圆心O₁，中园圆心O₂，小圆O₃，小圆半径y，中圆半径x，过O点作ON⊥AB于N，根据相切两圆的性质求出则OO₁、OO₃、O₁N、O₃N的长，由勾股定理得到方程求出xy=3（x+y），根据已知求出xy=48，代入即可求出AB．

解答：解：设最大圆的圆心O₁，中园圆心O₂，小圆O₃，小圆半径y，中圆半径x，过O点作ON⊥AB于N，则OO₁=x+y-3 OO₃=y+3 O₁N=O₁P+PN=X-Y+3，O₃N=Y-3，由勾股定理根据ON²=OO₁²-O₁N²=OO₃²-O₃N²，
∴（x+y-3）²-（x-y+3）²=（y+3）²-（y-3）²，
解方程得：xy=3（x+y），
因为图中阴影部分的面积是39π，
所以

1

2

[π（x+y）²-πx²-πy²]-9π=39π，∴xy=48，x+y=16，
∴AB=32，故答案为：32．

点评：本题主要考查对相切两圆的性质，勾股定理等知识点的理解和掌握，能推出xy=3（x+y）和xy=48是解此题的关键．