题目内容
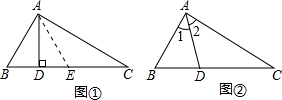 我们知道,利用三角形全等可以证明两条线段相等.但是我们会碰到这样的“和差”问题:“如图①,AD为△ABC的高,∠ABC=2∠C,证明:CD=AB+BD”.我们可以用“截长、补短”的方法将这类问题转化为证明两条线段相等的问题:在CD上截取DE=BD,连结AE.
我们知道,利用三角形全等可以证明两条线段相等.但是我们会碰到这样的“和差”问题:“如图①,AD为△ABC的高,∠ABC=2∠C,证明:CD=AB+BD”.我们可以用“截长、补短”的方法将这类问题转化为证明两条线段相等的问题:在CD上截取DE=BD,连结AE.(1)请补写完这个证明:
(2)运用上述方法证明:如图②,AD平分∠BAC,∠ABC=2∠C,证明:BD=AC-AB.
分析:(1)在CD上截取DE=BD,连结AE,推出AB=AE,根据∠B=2∠C,∠AEB=∠C+∠EAC求出∠C=∠EAC,推出EC=AE=AB,即可得出答案.
(2)证△BAD≌△EAD,推出DE=BD,∠B=∠AED,推出∠C=∠EDC,求出DE=EC=DB,即可得出答案.
(2)证△BAD≌△EAD,推出DE=BD,∠B=∠AED,推出∠C=∠EDC,求出DE=EC=DB,即可得出答案.
解答:(1)证明:在CD上截取DE=BD,连结AE,
∵AD⊥BC,
∴AB=AE,
∴∠B=∠AEB,
∵∠B=2∠C,∠AEB=∠C+∠EAC,
∴∠C=∠EAC,
∴EC=AE=AB,
∴CD=CE+DE=AB+BD.
(2)证明:在AC上截取AE=AB,连接DE,
∵AD平分∠BAC,
∴∠1=∠2,
在△BAD和△EAD中
∴△BAD≌△EAD,
∴DE=BD,∠B=∠AED,
∵∠B=2∠C,∠AEB=∠C+∠EDC,
∴∠C=∠EDC,
∴DE=EC=DB,
∵AC-AE=EC,EC=BD,AE=AB,
∴BD=AC-AB.
∵AD⊥BC,
∴AB=AE,
∴∠B=∠AEB,
∵∠B=2∠C,∠AEB=∠C+∠EAC,
∴∠C=∠EAC,
∴EC=AE=AB,
∴CD=CE+DE=AB+BD.

(2)证明:在AC上截取AE=AB,连接DE,
∵AD平分∠BAC,
∴∠1=∠2,
在△BAD和△EAD中
|
∴△BAD≌△EAD,
∴DE=BD,∠B=∠AED,
∵∠B=2∠C,∠AEB=∠C+∠EDC,
∴∠C=∠EDC,
∴DE=EC=DB,
∵AC-AE=EC,EC=BD,AE=AB,
∴BD=AC-AB.
点评:本题考查了等腰三角形的性质和判定,全等三角形的性质和判定,三角形外角性质的应用,关键是能正确作出辅助线.

练习册系列答案
相关题目
