题目内容
 如图A、B两点的坐标分别为A(18,0),B(8,6)点P、Q同时出发分别作匀速运动,其中点P从A出发沿AO向终点O运动,速度为每秒3个单位;点Q从O出发沿OB向终点B运动,速度为每秒2个单位,当这两点有一点到达自己的终点时,另一点也停止运动.
如图A、B两点的坐标分别为A(18,0),B(8,6)点P、Q同时出发分别作匀速运动,其中点P从A出发沿AO向终点O运动,速度为每秒3个单位;点Q从O出发沿OB向终点B运动,速度为每秒2个单位,当这两点有一点到达自己的终点时,另一点也停止运动.(1)坐标平面内是否存在点C,使以O、A、C为顶点的三角形与△OAB全等?请直接写出点C的坐标.
(2)设从出发起,运动了t秒钟,以O、P、Q为顶点的三角形与△OAB相似,求出此时t的值;
(3)是否存在t,使△OPQ为等腰三角形?若存在,求出运动的时间t;不存在,说明理由.
分析:(1)当△OAC≌△OAB时,C与B关于x轴对称;当△OAC≌△AOB时,点C可能在第一象限,也可能在第四象限,根据全等三角形的面积相等先求出点C的纵坐标,进而求出点C的横坐标;
(2)如果以O、P、Q为顶点的三角形与△OAB相似,由于∠POQ=∠AOB,那么O与O是对应点,所以分两种情况进行讨论:①△POQ∽△AOB;②△POQ∽△BOA;根据相似三角形对应边成比例列出比例式,即可求解;
(3)分三种情况进行讨论:①OP=OQ;②PO=PQ;③QO=QP.
(2)如果以O、P、Q为顶点的三角形与△OAB相似,由于∠POQ=∠AOB,那么O与O是对应点,所以分两种情况进行讨论:①△POQ∽△AOB;②△POQ∽△BOA;根据相似三角形对应边成比例列出比例式,即可求解;
(3)分三种情况进行讨论:①OP=OQ;②PO=PQ;③QO=QP.
解答: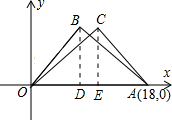 解:(1)坐标平面内存在点C,使以O、A、C为顶点的三角形与△OAB全等.理由如下:
解:(1)坐标平面内存在点C,使以O、A、C为顶点的三角形与△OAB全等.理由如下:
①当△OAC≌△OAB时,C与B关于x轴对称,此时点C的坐标为(8,-6);
②当△OAC≌△AOB时,点C可能在第一象限,也可能在第四象限,设点C的坐标为(x,y).
∵△OAC≌△AOB,
∴S△OAC=S△AOB,即
•OA•|y|=
•OA•6,
∴|y|=6,y=±6.
如果点C在第一象限,如图,过点B、C作x轴的垂线,垂足分别为D、E,则BD=CE=6,
∵△ACE≌△OBD(HL),
∴AE=OD=8,
∴OE=OA-AE=18-8=10,
∴此时点C的坐标为(10,6);
如果点C在第四象限,易求此时点C的坐标为(10,-6);
即满足条件的点C的坐标为(8,-6)或(10,6)或(10,6);
 (2)设从出发起,运动了t秒钟,以O、P、Q为顶点的三角形与△OAB相似.
(2)设从出发起,运动了t秒钟,以O、P、Q为顶点的三角形与△OAB相似.
∵AP=3t,OQ=2t,
∴OP=18-3t.
分两种情况:
①如果△POQ∽△AOB,那么
=
,
=
,
解得t=
;
②如果△POQ∽△BOA,那么
=
,
=
,
解得t=
;
故以O、P、Q为顶点的三角形与△OAB相似时,t的值为
秒或
秒;
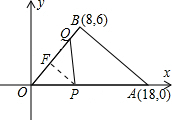 (3)△OPQ为等腰三角形时,分三种情况:
(3)△OPQ为等腰三角形时,分三种情况:
①如果OP=OQ,那么18-3t=2t,t=
;
②如果PO=PQ,如图,过点P作PF⊥OQ于F,则OF=FQ=
OQ=
•2t=t.
∵在Rt△OPF中,∠OFP=90°,
∴OF=OP•cos∠POF=(18-3t)•
=
(18-3t),
∴t=
(18-3t),
解得t=
;
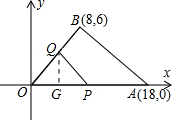 ③如果QO=QP,如图,过点Q作QG⊥OP于G,则OG=GP=
③如果QO=QP,如图,过点Q作QG⊥OP于G,则OG=GP=
OP=
•(18-3t)=9-
t.
∵在Rt△OQG中,∠OGQ=90°,
∴OG=OQ•cos∠QOG=2t•
=
t,
∴9-
t=
t,
解得t=
.
综上所述,所求t的值为
秒或
秒或
秒.
 解:(1)坐标平面内存在点C,使以O、A、C为顶点的三角形与△OAB全等.理由如下:
解:(1)坐标平面内存在点C,使以O、A、C为顶点的三角形与△OAB全等.理由如下:①当△OAC≌△OAB时,C与B关于x轴对称,此时点C的坐标为(8,-6);
②当△OAC≌△AOB时,点C可能在第一象限,也可能在第四象限,设点C的坐标为(x,y).
∵△OAC≌△AOB,
∴S△OAC=S△AOB,即
| 1 |
| 2 |
| 1 |
| 2 |
∴|y|=6,y=±6.
如果点C在第一象限,如图,过点B、C作x轴的垂线,垂足分别为D、E,则BD=CE=6,
∵△ACE≌△OBD(HL),
∴AE=OD=8,
∴OE=OA-AE=18-8=10,
∴此时点C的坐标为(10,6);
如果点C在第四象限,易求此时点C的坐标为(10,-6);
即满足条件的点C的坐标为(8,-6)或(10,6)或(10,6);
 (2)设从出发起,运动了t秒钟,以O、P、Q为顶点的三角形与△OAB相似.
(2)设从出发起,运动了t秒钟,以O、P、Q为顶点的三角形与△OAB相似.∵AP=3t,OQ=2t,
∴OP=18-3t.
分两种情况:
①如果△POQ∽△AOB,那么
| OP |
| OA |
| OQ |
| OB |
| 18-3t |
| 18 |
| 2t |
| 10 |
解得t=
| 30 |
| 11 |
②如果△POQ∽△BOA,那么
| OP |
| OB |
| OQ |
| OA |
| 18-3t |
| 10 |
| 2t |
| 18 |
解得t=
| 162 |
| 37 |
故以O、P、Q为顶点的三角形与△OAB相似时,t的值为
| 30 |
| 11 |
| 162 |
| 37 |
 (3)△OPQ为等腰三角形时,分三种情况:
(3)△OPQ为等腰三角形时,分三种情况:①如果OP=OQ,那么18-3t=2t,t=
| 18 |
| 5 |
②如果PO=PQ,如图,过点P作PF⊥OQ于F,则OF=FQ=
| 1 |
| 2 |
| 1 |
| 2 |
∵在Rt△OPF中,∠OFP=90°,
∴OF=OP•cos∠POF=(18-3t)•
| 8 |
| 10 |
| 4 |
| 5 |
∴t=
| 4 |
| 5 |
解得t=
| 72 |
| 17 |
 ③如果QO=QP,如图,过点Q作QG⊥OP于G,则OG=GP=
③如果QO=QP,如图,过点Q作QG⊥OP于G,则OG=GP=| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∵在Rt△OQG中,∠OGQ=90°,
∴OG=OQ•cos∠QOG=2t•
| 8 |
| 10 |
| 8 |
| 5 |
∴9-
| 3 |
| 2 |
| 8 |
| 5 |
解得t=
| 90 |
| 31 |
综上所述,所求t的值为
| 18 |
| 5 |
| 72 |
| 17 |
| 90 |
| 31 |
点评:本题考查全等三角形、相似三角形、等腰三角形的性质,综合性较强,难度适中.运用数形结合及分类讨论是解题的关键.

练习册系列答案
相关题目
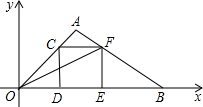 如图,点A的坐标为(1,1),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,若以B,E,F为顶点的三角形与△OFE相似,B点的坐标是
如图,点A的坐标为(1,1),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,若以B,E,F为顶点的三角形与△OFE相似,B点的坐标是 如图,点D的坐标为(0,1),直线y=-2
如图,点D的坐标为(0,1),直线y=-2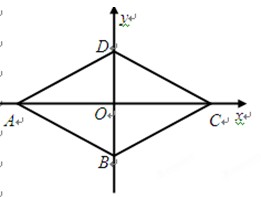
 (2)将
(2)将