题目内容
现用总长为80m的建筑材料,围成一个扇形花坛,当扇形半径为 时,可使花坛的面积最大.
【答案】分析:设扇形的半径为xm,则弧长为(80-2x)m,根据扇形的面积公式:S= lR得到S=
lR得到S= •x•(80-2x)=-x2+40x,然后再根据二次函数的最值问题求得当x为20时,S最大.
•x•(80-2x)=-x2+40x,然后再根据二次函数的最值问题求得当x为20时,S最大.
解答:解:设扇形的半径为xm,则弧长为(80-2x)m,
根据题意有,S= •x•(80-2x)=-x2+40x,
•x•(80-2x)=-x2+40x,
∵a=-1<0,
∴S有最大值.
当x=-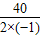 =20,S有最大值.
=20,S有最大值.
所以扇形半径为20m时,可使花坛的面积最大.
故答案为20m.
点评:本题考查了扇形的面积公式:S=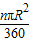 ,其中n为扇形的圆心角的度数,R为圆的半径),或S=
,其中n为扇形的圆心角的度数,R为圆的半径),或S= lR,l为扇形的弧长,R为半径.也考查了二次函数的最值问题.
lR,l为扇形的弧长,R为半径.也考查了二次函数的最值问题.
 lR得到S=
lR得到S= •x•(80-2x)=-x2+40x,然后再根据二次函数的最值问题求得当x为20时,S最大.
•x•(80-2x)=-x2+40x,然后再根据二次函数的最值问题求得当x为20时,S最大.解答:解:设扇形的半径为xm,则弧长为(80-2x)m,
根据题意有,S=
 •x•(80-2x)=-x2+40x,
•x•(80-2x)=-x2+40x,∵a=-1<0,
∴S有最大值.
当x=-
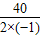 =20,S有最大值.
=20,S有最大值.所以扇形半径为20m时,可使花坛的面积最大.
故答案为20m.
点评:本题考查了扇形的面积公式:S=
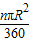 ,其中n为扇形的圆心角的度数,R为圆的半径),或S=
,其中n为扇形的圆心角的度数,R为圆的半径),或S= lR,l为扇形的弧长,R为半径.也考查了二次函数的最值问题.
lR,l为扇形的弧长,R为半径.也考查了二次函数的最值问题. 
练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 附加题:现有总长为8m的建筑材料,用这些建筑材料围成一个扇形的花坛(如图),当这个扇形的半径为多少时,可以使这个扇形花坛的面积最大并求最大面积.
附加题:现有总长为8m的建筑材料,用这些建筑材料围成一个扇形的花坛(如图),当这个扇形的半径为多少时,可以使这个扇形花坛的面积最大并求最大面积.