题目内容
【题目】如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=﹣ ![]() x+1与y轴交于点D.
x+1与y轴交于点D. 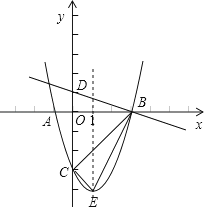
(1)求抛物线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.
【答案】
(1)
解:∵抛物线y=ax2+bx﹣3,
∴c=﹣3,
∴C(0,﹣3),
∴OC=3,
∵BO=OC=3AO,
∴BO=3,AO=1,
∴B(3,0),A(﹣1,0),
∵该抛物线与x轴交于A、B两点,
∴ ![]() ,
,
∴ ![]() ,
,
∴抛物线解析式为y=x2﹣2x﹣3
(2)
证明:由(1)知,抛物线解析式为y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴E(1,﹣4),
∵B(3,0),A(﹣1,0),C(0,﹣3),
∴BC=3 ![]() ,BE=2
,BE=2 ![]() ,CE=
,CE= ![]() ,
,
∵直线y=﹣ ![]() x+1与y轴交于点D,
x+1与y轴交于点D,
∴D(0,1),
∵B(3,0),
∴OD=1,OB=3,BD= ![]() ,
,
∴ ![]() ,
, ![]() ,
, ![]() ,
,
∴ ![]() ,
,
∴△BCE∽△BDO
(3)
解:存在,
理由:设P(1,m),
∵B(3,0),C(0,﹣3),
∴BC=3 ![]() ,PB=
,PB= ![]() ,PC=
,PC= ![]() ,
,
∵△PBC是等腰三角形,
①当PB=PC时,
∴ ![]() =
= ![]() ,
,
∴m=﹣1,
∴P(1,﹣1),
②当PB=BC时,
∴3 ![]() =
= ![]() ,
,
∴m=± ![]() ,
,
∴P(1, ![]() )或P(1,﹣
)或P(1,﹣ ![]() ),
),
③当PC=BC时,
∴3 ![]() =
= ![]() ,
,
∴m=﹣3± ![]() ,
,
∴P(1,﹣3+ ![]() )或P(1,﹣3﹣
)或P(1,﹣3﹣ ![]() ),
),
∴符合条件的P点坐标为P(1,﹣1)或P(1, ![]() )或P(1,﹣
)或P(1,﹣ ![]() )或P(1,﹣3+
)或P(1,﹣3+ ![]() )或P(1,﹣3﹣
)或P(1,﹣3﹣ ![]() )
)
【解析】(1)先求出点C的坐标,在由BO=OC=3AO,确定出点B,A的坐标,最后用待定系数法求出抛物线解析式;(2)先求出点A,B,C,D,E的坐标,从而求出BC=3 ![]() ,BE=2
,BE=2 ![]() ,CE=
,CE= ![]() ,OD=1,OB=3,BD=
,OD=1,OB=3,BD= ![]() ,求出比值,得到
,求出比值,得到 ![]() 得出结论;(3)设出点P的坐标,表示出PB,PC,求出BC,分三种情况计算即可.此题是二次函数综合题,主要考查了点的坐标的确定方法,两点间的距离公式,待定系数法,等腰三角形的性质,相似三角形的判定,解本题的关键是判断△BCE∽△BDO.难点是分类.
得出结论;(3)设出点P的坐标,表示出PB,PC,求出BC,分三种情况计算即可.此题是二次函数综合题,主要考查了点的坐标的确定方法,两点间的距离公式,待定系数法,等腰三角形的性质,相似三角形的判定,解本题的关键是判断△BCE∽△BDO.难点是分类.

【题目】某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:
组号 | 分组 | 频数 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |
(1)求a的值;
(2)若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2 , 在第四组内的两名选手记为:B1、B2 , 从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果).