题目内容
已知⊙O1和⊙O2相交于A、B两点，过点A作⊙O1的弦AC切⊙O2于点A，作⊙O2的弦AD切⊙O1于点A，设BC=a，BD=b，则公共弦AB的长是分析：由于AD是切线，利用弦切角定理可得∠BAD=∠ACB，同理可证∠CAB=∠ADB，那么易证△ABC∽△DAB，从而有AB：BD=BC：AB，那么可求AB．
解答：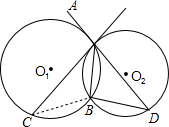
解：如右图所示，连接BC，
∵AD是⊙O1的切线，
∴∠BAD=∠ACB，
同理有∠CAB=∠ADB，
∴△ABC∽△DAB，
∴AB：BD=BC：AB，
∴AB2=ab，
∴AB=
．
故答案是
．
解：如右图所示，连接BC，∵AD是⊙O1的切线，
∴∠BAD=∠ACB，
同理有∠CAB=∠ADB，
∴△ABC∽△DAB，
∴AB：BD=BC：AB，
∴AB2=ab，
∴AB=
| ab |
故答案是
| ab |
点评：本题考查了弦切角定理、相似三角形的判定和性质．关键是证明△ABC∽△DAB．
练习册系列答案
阅读快车系列答案
相关题目