题目内容
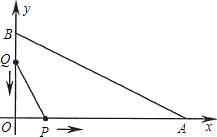
【题目】在平面直角坐标系中,已知OA=10cm,OB=5cm,点P从点O开始沿OA边向点A以2cm/s的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤5),
(1)用含t的代数式表示:线段PO= cm;OQ= cm.
(2)当t为何值时,四边形PABQ的面积为19cm2.
(3)当△POQ与△AOB相似时,求出t的值.
【答案】(1)2t,(5﹣t),(2)当t=2或3时,四边形PABQ的面积为19cm2.(3)当t=![]() 或1时,△POQ与△AOB相似.
或1时,△POQ与△AOB相似.
【解析】
(1)根据路程=速度×时间可求解;
(2)由面积和差关系列出方程求解;
(3)根据△POQ与△AOB相似分两种情形列出方程即可解决问题.
解:(1)OP=2tcm,OQ=(5﹣t)cm,
故答案为:2t,(5﹣t),
(2)∵S四边形PABQ=S△ABO﹣S△PQO,
∴19=![]() ×10×5﹣
×10×5﹣![]() ×2t×(5﹣t),
×2t×(5﹣t),
∴t=2或3,
∴当t=2或3时,四边形PABQ的面积为19cm2.
(3)∵△POQ与△AOB相似,∠POQ=∠AOB=90°,
∴![]() 或
或![]()
①当![]() ,则
,则![]() ,
,
∴t=![]() ,
,
②当![]() 时,则
时,则![]() ,
,
∴t=1,
∴当t=![]() 或1时,△POQ与△AOB相似.
或1时,△POQ与△AOB相似.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目