题目内容
若已知正方形的面积为4x2+4xy+y2（x＞0，y＞O），则边长是
2x+y
2x+y
．分析：根据完全平方式配方，再根据算术平方根求解即可．
解答：解：4x2+4xy+y2
=（2x）2+2×2x•y+y2
=（2x+y）2，
∴正方形的边长是：2x+y．
故答案为：2x+y
=（2x）2+2×2x•y+y2
=（2x+y）2，
∴正方形的边长是：2x+y．
故答案为：2x+y
点评：本题考查了完全平方式与算术平方根的定义，利用完全平方公式配方是解题的关键．
练习册系列答案
相关题目
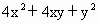，则边长是___________．
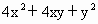，则边长是___________．