题目内容
某医药研究所研制了一种新药,在试验药效时发现:成人按规定剂量服用后,检测到从第5分钟起每分钟每毫升血液中含药量增加0.2微克,第100分钟达到最高,接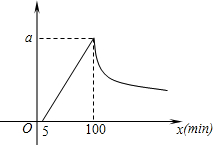 着开始衰退.血液中含药量y(微克)与时间x(分钟)的函数关系如图.并发现衰退时y与x成反比例函数关系.
着开始衰退.血液中含药量y(微克)与时间x(分钟)的函数关系如图.并发现衰退时y与x成反比例函数关系.
(1)a=________;
(2)当5≤x≤100时,y与x之间的函数关系式为________;当x>100时,y与x之间的函数关系式为________;
(3)如果每毫升血液中含药量不低于10微克时是有效的,求出一次服药后的有效时间多久?
解:(1)a=0.2×(100-5)=19;
(2)当5≤x≤100时,设y与x之间的函数关系式为y=k1x+b
∵经过点(5,0),(100,19)
∴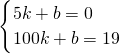
解得:,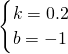
∴解析式为y=0.2x-1;
当x>100时,y与x之间的函数关系式为y= ,
,
∵经过点(100,19),
∴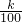 =19
=19
解得:k=1900,
∴函数的解析式为y=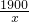 ;
;
(3)令y=0.2x-1=10解得:x=55,
令y=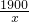 =10,解得:x=190
=10,解得:x=190
∴190-55=135分钟,
∴服药后能持续135分钟;
分析:(1)利用第5分钟起每分钟每毫升血液中含药量增加0.2微克即可得到第100分钟相应的a值;
(2)分别代入直线和曲线的一般形式,利用待定系数法求得函数的解析式即可;
(3)分别令两个函数值为10求得相应的时间后相减即可得到结果.
点评:本题主要考查了反比例函数与一次函数的实际应用,根据已知点得出函数的解析式是解题关键.
(2)当5≤x≤100时,设y与x之间的函数关系式为y=k1x+b
∵经过点(5,0),(100,19)
∴
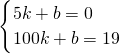
解得:,
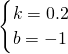
∴解析式为y=0.2x-1;
当x>100时,y与x之间的函数关系式为y=
 ,
,∵经过点(100,19),
∴
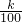 =19
=19解得:k=1900,
∴函数的解析式为y=
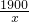 ;
;(3)令y=0.2x-1=10解得:x=55,
令y=
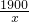 =10,解得:x=190
=10,解得:x=190∴190-55=135分钟,
∴服药后能持续135分钟;
分析:(1)利用第5分钟起每分钟每毫升血液中含药量增加0.2微克即可得到第100分钟相应的a值;
(2)分别代入直线和曲线的一般形式,利用待定系数法求得函数的解析式即可;
(3)分别令两个函数值为10求得相应的时间后相减即可得到结果.
点评:本题主要考查了反比例函数与一次函数的实际应用,根据已知点得出函数的解析式是解题关键.

练习册系列答案
相关题目
 着开始衰退.血液中含药量y(微克)与时间x(分钟)的函数关系如图.并发现衰退时y与x成反比例函数关系.
着开始衰退.血液中含药量y(微克)与时间x(分钟)的函数关系如图.并发现衰退时y与x成反比例函数关系.