题目内容
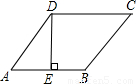
 如图,菱形ABCD是周长为20cm,DE⊥AB,垂足为E,cosA=
如图,菱形ABCD是周长为20cm,DE⊥AB,垂足为E,cosA= ,则下列结论中:①DE=3cm;②EB=1cm;③S菱形ABCD=15cm2;④对角线AC=1.5BD.正确的个数为
,则下列结论中:①DE=3cm;②EB=1cm;③S菱形ABCD=15cm2;④对角线AC=1.5BD.正确的个数为
- A.4个
- B.3个
- C.2个
- D.1个
B
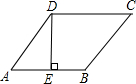
分析:如图,由菱形ABCD,可得AB=BC=CD=AD,AC⊥BD,OA=OC,OB=OD;又由菱形ABCD是周长为20cm,可得AD=5cm;又因为DE⊥AB,cosA= ,易得DE=3cm,AE=4cm,可得EB=1cm;可得BD=
,易得DE=3cm,AE=4cm,可得EB=1cm;可得BD= cm,易得AC=
cm,易得AC=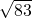 cm.
cm.
解答: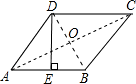 解:连接AC与BD,
解:连接AC与BD,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD,OA=OC,OB=OD,
又∵菱形ABCD是周长为20cm,
∴AD=5cm,
又∵DE⊥AB,cosA= ,
,
∴DE=3cm,AE=4cm,
∴EB=1cm,
∴BD=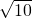 cm,
cm,
∴AC=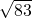 cm.
cm.
∴S菱形ABCD= cm2,
cm2,
∴①②③正确.
故选B.
点评:此题考查了菱形的性质:菱形的四条边都相等;菱形的对角线互相平分且相等;菱形的面积等于对角线积的一半.此题还要注意结合三角函数求解.
分析:如图,由菱形ABCD,可得AB=BC=CD=AD,AC⊥BD,OA=OC,OB=OD;又由菱形ABCD是周长为20cm,可得AD=5cm;又因为DE⊥AB,cosA=
 ,易得DE=3cm,AE=4cm,可得EB=1cm;可得BD=
,易得DE=3cm,AE=4cm,可得EB=1cm;可得BD= cm,易得AC=
cm,易得AC=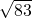 cm.
cm.解答:
 解:连接AC与BD,
解:连接AC与BD,∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD,OA=OC,OB=OD,
又∵菱形ABCD是周长为20cm,
∴AD=5cm,
又∵DE⊥AB,cosA=
 ,
,∴DE=3cm,AE=4cm,
∴EB=1cm,
∴BD=
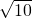 cm,
cm,∴AC=
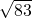 cm.
cm.∴S菱形ABCD=
 cm2,
cm2,∴①②③正确.
故选B.
点评:此题考查了菱形的性质:菱形的四条边都相等;菱形的对角线互相平分且相等;菱形的面积等于对角线积的一半.此题还要注意结合三角函数求解.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
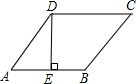 如图,菱形ABCD是周长为20cm,DE⊥AB,垂足为E,cosA=
如图,菱形ABCD是周长为20cm,DE⊥AB,垂足为E,cosA=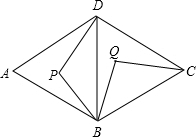 如图:菱形ABCD是由两个正三角形拼成的,点P在△ABD内任一点,现把△BPD绕点B旋转到△BQC的位置.则
如图:菱形ABCD是由两个正三角形拼成的,点P在△ABD内任一点,现把△BPD绕点B旋转到△BQC的位置.则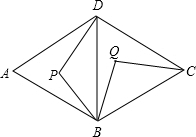 如图:菱形ABCD是由两个正三角形拼成的,点P在△ABD内任一点,现把△BPD绕点B旋转到△BQC的位置.则
如图:菱形ABCD是由两个正三角形拼成的,点P在△ABD内任一点,现把△BPD绕点B旋转到△BQC的位置.则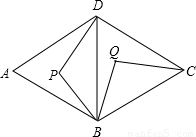
 ,则下列结论中:①DE=3cm;②EB=1cm;③S菱形ABCD=15cm2;④对角线AC=1.5BD.正确的个数为( )
,则下列结论中:①DE=3cm;②EB=1cm;③S菱形ABCD=15cm2;④对角线AC=1.5BD.正确的个数为( )