题目内容

如图，已知小正方形ABCD的面积为1，把它的各边延长一倍得到新正方形A1B1C1D1；把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2；以此进行下去…，则正方形AnBnCnDn的面积为（　　）
A、（
5
）n
B、5n
C、5n-1
D、5n+1
练习册系列答案
相关题目
如图，△ABC中，∠ABC=90°，AB=8，BC=6，点F，D是直线AC上的两个动点，且FD=AC．点B和点E分别在直线AD的两侧，AB=DE，AB∥DE，当四边形BCEF是菱形时AF等于（　　）
A、
7
5
B、
14
5
C、5
D、4
如图，矩形ABCD中，AD=2AB，E、F、G、H分别是AB，BC，CD，AD边上的点，EG⊥FH，FH=2
2
，则四边形EFGH的面积为（　　）
A、8
2
B、8
C、12
2
D、24
如图，四边形ABCD，AEFG都是正方形，点E，G分别在AB，AD上，连接FC，过点E作EH∥FC交BC于点H．若AB=4，AE=1，则BH的长为（　　）
A、1
B、2
C、3
D、3
2
如图，甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动，甲点依顺时针方向环行，乙点依逆时针方向环行，若乙的速度是甲的速度的4倍，则它们第2014次相遇在边（　　）
A、AB上B、BC上C、CD上D、DA上
如果要证明平行四边形ABCD为正方形，那么我们需要在四边形ABCD是平行四边形的基础上，进一步证明（　　）
A、AB=AD且AC⊥BDB、AB=AD且AC=BDC、∠A=∠B且AC=BDD、AC和BD互相垂直平分
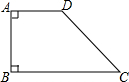如图，在直角梯形ABCD中，AD∥BC，∠A=90°，DC=4，cosC=
4
5
，那么AB边的长为（　　）
A、4
B、
12
5
C、
9
5
D、5
小蓁与她的五位朋友参加保龄球比赛，如图为她们六人所得分数的盒状图．若小蓁所得到的分数恰为她们六人的平均分数，则小蓁得到多少分？（　　）
A、165B、169C、170D、175
有一组数据：1，3，3，4，5，这组数据的众数为（　　）
A、1B、3C、4D、5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网