题目内容
 铁道口的栏杆如图,短臂OD长1.25 m,长臂OE长16.5 m,当短臂端点下降0.85m(AD长)时,求长臂端点升高多少m(BE的长)?(不计杆的高度)
铁道口的栏杆如图,短臂OD长1.25 m,长臂OE长16.5 m,当短臂端点下降0.85m(AD长)时,求长臂端点升高多少m(BE的长)?(不计杆的高度)
解:∵∠DAO=∠EBO=90°,∠AOD=∠BOE,
∴△AOD∽△BOE.
∴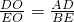 ,
,
即 =
= ,
,
∴BE=11.22m.
答:长臂端点升高11.22m.
分析:依题意,易证△AOD∽△BOE,可利用对应边成比例求解线段的长度.
点评:能够运用相似三角形的性质解决一些实际计算问题.
∴△AOD∽△BOE.
∴
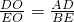 ,
,即
 =
= ,
,∴BE=11.22m.
答:长臂端点升高11.22m.
分析:依题意,易证△AOD∽△BOE,可利用对应边成比例求解线段的长度.
点评:能够运用相似三角形的性质解决一些实际计算问题.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 铁道口的栏杆如图,短臂OD长1.25 m,长臂OE长16.5 m,当短臂端点下降0.85m(AD长)时,求长臂端点升高多少m(BE的长)?(不计杆的高度)
铁道口的栏杆如图,短臂OD长1.25 m,长臂OE长16.5 m,当短臂端点下降0.85m(AD长)时,求长臂端点升高多少m(BE的长)?(不计杆的高度)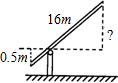 如图,铁道口的栏杆短臂长1m,长臂长16m.当短臂端点下降0.5m时,长臂端点升高( )
如图,铁道口的栏杆短臂长1m,长臂长16m.当短臂端点下降0.5m时,长臂端点升高( )