题目内容
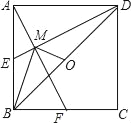
如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:
①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM= MF.其中正确结论的是( )
MF.其中正确结论的是( )
A. ①③④ B. ②④⑤ C. ①③④⑤ D. ①③⑤
练习册系列答案
相关题目
题目内容
如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:
①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM= MF.其中正确结论的是( )
MF.其中正确结论的是( )

A. ①③④ B. ②④⑤ C. ①③④⑤ D. ①③⑤