ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎRtΓςABC÷–Θ§ΓœCBA=90ΓψΘ§ΓœCABΒΡΫ«ΤΫΖ÷œΏAPΚΆΓœACBΆβΫ«ΒΡΤΫΖ÷œΏCFœύΫΜ”ΎΒψDΘ§ADΫΜCB”ΎΒψPΘ§CFΫΜABΒΡ―”≥ΛœΏ”ΎΒψFΘ§ΙΐΒψDΉςDEΓΆCFΫΜCBΒΡ―”≥ΛœΏ”ΎΒψGΘ§ΫΜABΒΡ―”≥ΛœΏ”ΎΒψEΘ§Ν§Ϋ”CE≤Δ―”≥ΛΫΜFG”ΎΒψHΘ§‘ρœ¬Ν–Ϋα¬έΘΚΔΌΓœCDA=45ΓψΘΜΔΎAF-CG=CAΘΜΔέDE=DCΘΜΔήFH=CD+GHΘΜΔίCF=2CD+EGΘ°Τδ÷–’ΐ»ΖΒΡ”–Θ®ΓΓΓΓΘ©
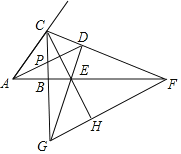
A. ΔΌΔΎΔή B. ΔΌΔΎΔέ C. ΔΌΔΎΔήΔί D. ΔΌΔΎΔέΔί
ΓΨ¥πΑΗΓΩD
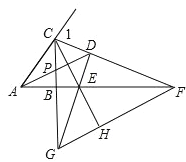
ΓΨΫβΈωΓΩ ‘ΧβΫβΈωΘΚΔΌάϊ”ΟΙΪ ΫΘΚΓœCDA=![]() ΓœABC=45ΓψΘ§ΔΌ’ΐ»ΖΘΜ
ΓœABC=45ΓψΘ§ΔΌ’ΐ»ΖΘΜ
ΔΎ»γΆΦΘΚ―”≥ΛGD”κACΫΜ”ΎΒψP'Θ§

”…»ΐœΏΚœ“ΜΩ…÷ΣCG=CP'Θ§
ΓΏΓœADC=45ΓψΘ§DGΓΆCFΘ§
ΓύΓœEDA=ΓœCDA=45ΓψΘ§
ΓύΓœADP=ΓœADFΘ§
ΓύΓςADP'Γ’ΓςADFΘ®ASAΘ©Θ§
ΓύAF=AP'=AC+CP'=AC+CGΘ§Ι ΔΎ’ΐ»ΖΘΜ
Δέ»γΆΦΘΚ
ΓΏΓœEDA=ΓœCDAΘ§
ΓœCAD=ΓœEADΘ§
¥”ΕχΓςCADΓ’ΓςEADΘ§
Ι DC=DEΘ§Δέ’ΐ»ΖΘΜ
ΔήΓΏBFΓΆCGΘ§GDΓΆCFΘ§
ΓύEΈΣΓςCGF¥Ι–ΡΘ§
ΓύCHΓΆGFΘ§«“ΓςCDEΓΔΓςCHFΓΔΓςGHEΨυΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
ΓύHF=CH=EH+CE=GH+CE=GH+![]() CDΘ§Ι Δή¥μΈσΘΜ
CDΘ§Ι Δή¥μΈσΘΜ
Δί»γΆΦΘΚΉςMEΓΆCEΫΜCF”ΎΒψMΘ§
‘ρΓςCEMΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§¥”ΕχCD=DMΘ§CM=2CDΘ§EM=ECΘ§
ΓΏΓœMFE=ΓœCGEΘ§
ΓœCEG=ΓœEMF=135ΓψΘ§
ΓύΓςEMFΓ’ΓςCEGΘ®AASΘ©Θ§
ΓύGE=MFΘ§
ΓύCF=CM+MF=2CD+GEΘ§
Ι Δί’ΐ»ΖΘΜ
Ι ―ΓD

