题目内容
(2002•武汉)已知抛物线 交x轴于A(x1,0)、B(x2,0),交y轴于C点,且x1<0<x2,(AO+OB)2=12CO+1.
交x轴于A(x1,0)、B(x2,0),交y轴于C点,且x1<0<x2,(AO+OB)2=12CO+1.(1)求抛物线的解析式;
(2)在x轴的下方是否存在着抛物线上的点P,使∠APB为锐角?若存在,求出P点的横坐标的范围;若不存在,请说明理由.
【答案】分析:(1)可根据(AO+OB)2=12CO+1以及一元二次方程根与系数的关系来求出m的值,进而可确定出抛物线的解析式;
(2)本题的关键是找出∠APB为直角时,P点的位置,根据(1)的抛物线不难得出A,B,C三点的坐标为(-1,0)(4,0)
(0,-2).如果∠APB为直角,那么点P必为以AB为直径的圆与抛物线的交点.据此可判断出∠APB时,P点横坐标的范围.
解答: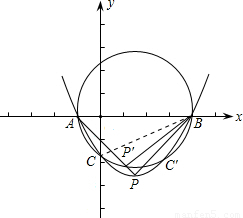 解:(1)抛物线y=
解:(1)抛物线y= x2-
x2- mx-2m交x轴于A(a,0)和B(b,0),
mx-2m交x轴于A(a,0)和B(b,0),
所以a+b=3m,a•b=-4m,
∵抛物线开口向上,与X轴有两个交点,
∴C点在Y轴下半轴上,所以点C(0,-2m),-2m<0,所以m>0,
AO+OB=|a-b|,OC=|-2m|=2m,
所以(AO+OB)2=(a-b)2=(a+b)-4ab=9m2+16m,
12OC+1=24m+1,
∴9m2+16m=24m+1,
9m2-8m-1=0,
m=1或m=- <0,舍去,
<0,舍去,
∴m=1,
即抛物线的解析式为:y= x2-
x2- x-2;
x-2;
(2)易知:A点坐标为(-1,0),B点坐标为(4,0),C点坐标为(0,-2),
连接AC,BC,AC=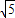 ,BC=2
,BC=2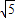 ,AB=5,
,AB=5,
∴AC2+BC2=AB2,
∴∠ACB=90°,
设C关于抛物线对称轴的对称点为C′,
那么C′坐标为(3,-2),
根据抛物线的对称性可知:如果连接AC′、BC′,那么∠AC′B=90°,
因此如果以AB为直径作圆,那么此圆必过C,C′,
根据圆周角定理可知:x轴下方的半圆上任意一点和A、B组成的三角形都是直角三角形,
如果设P点横坐标为x,那么必有当0<x<3时,∠APB为锐角,
当-1<x<0或3<x<4时,∠APB为钝角.
点评:本题考查了一元二次方程根与系数的关系,二次函数解析式的确定等知识点.要注意的是(2)中结合圆周角的相关知识来理解问题可使问题简化.
(2)本题的关键是找出∠APB为直角时,P点的位置,根据(1)的抛物线不难得出A,B,C三点的坐标为(-1,0)(4,0)
(0,-2).如果∠APB为直角,那么点P必为以AB为直径的圆与抛物线的交点.据此可判断出∠APB时,P点横坐标的范围.
解答:
 解:(1)抛物线y=
解:(1)抛物线y= x2-
x2- mx-2m交x轴于A(a,0)和B(b,0),
mx-2m交x轴于A(a,0)和B(b,0),所以a+b=3m,a•b=-4m,
∵抛物线开口向上,与X轴有两个交点,
∴C点在Y轴下半轴上,所以点C(0,-2m),-2m<0,所以m>0,
AO+OB=|a-b|,OC=|-2m|=2m,
所以(AO+OB)2=(a-b)2=(a+b)-4ab=9m2+16m,
12OC+1=24m+1,
∴9m2+16m=24m+1,
9m2-8m-1=0,
m=1或m=-
 <0,舍去,
<0,舍去,∴m=1,
即抛物线的解析式为:y=
 x2-
x2- x-2;
x-2;(2)易知:A点坐标为(-1,0),B点坐标为(4,0),C点坐标为(0,-2),
连接AC,BC,AC=
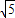 ,BC=2
,BC=2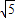 ,AB=5,
,AB=5,∴AC2+BC2=AB2,
∴∠ACB=90°,
设C关于抛物线对称轴的对称点为C′,
那么C′坐标为(3,-2),
根据抛物线的对称性可知:如果连接AC′、BC′,那么∠AC′B=90°,
因此如果以AB为直径作圆,那么此圆必过C,C′,
根据圆周角定理可知:x轴下方的半圆上任意一点和A、B组成的三角形都是直角三角形,
如果设P点横坐标为x,那么必有当0<x<3时,∠APB为锐角,
当-1<x<0或3<x<4时,∠APB为钝角.
点评:本题考查了一元二次方程根与系数的关系,二次函数解析式的确定等知识点.要注意的是(2)中结合圆周角的相关知识来理解问题可使问题简化.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
 交x轴于A(x1,0)、B(x2,0),交y轴于C点,且x1<0<x2,(AO+OB)2=12CO+1.
交x轴于A(x1,0)、B(x2,0),交y轴于C点,且x1<0<x2,(AO+OB)2=12CO+1.