题目内容
【题目】CD经过∠BCA顶点C的一条直线，CA=CB，E、F分别是直线CD上两点，且∠BEC=∠CFA=∠
，
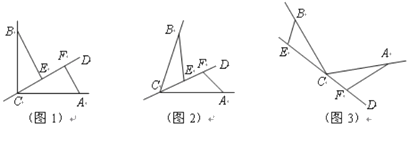
（1）若直线CD经过∠BCA的内部，且E、F在射线CD上，请解决下面两个问题：
①如图1，若∠BCA=90°,∠=90°，则BE_____CF；EF____
.（填“＞”“＜”或“=”）
②如图2，若0°＜∠BCA＜180°,请添加一个关于∠与∠BCA关系的条件__________,使①中的两个结论仍然成立，并证明两个结论成立.
（2）如图3，若直线CD经过∠BCA的外部，∠=∠BCA，请提出EF，BE，AF三条线段数量关系的合理猜想（不要求证明）.
【答案】（1）①=，=;②∠α+∠ACB=180°；（2）EF=BE+AF
【解析】
（1）①求出∠BEC=∠AFC=90°，∠CBE=∠ACF，根据AAS证△BCE≌△CAF，推出BE=CF，CE=AF即可；
②求出∠BEC=∠AFC，∠CBE=∠ACF，根据AAS证△BCE≌△CAF，推出BE=CF，CE=AF即可；
（2）求出∠BEC=∠AFC，∠CBE=∠ACF，根据AAS证△BCE≌△CAF，推出BE=CF，CE=AF即可．
解：（1）①如图1中，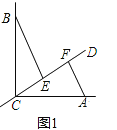
E点在F点的左侧，
∵BE⊥CD，AF⊥CD，∠ACB=90°，
∴∠BEC=∠AFC=90°，
∴∠BCE+∠ACF=90°，∠CBE+∠BCE=90°，
∴∠CBE=∠ACF，
在△BCE和△CAF中，
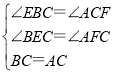
∴△BCE≌△CAF（AAS），
∴BE=CF，CE=AF，
∴EF=CF-CE=BE-AF，
当E在F的右侧时，同理可证EF=AF-BE，
∴EF=|BE-AF|
故答案为=，=;
②∠α+∠ACB=180°时，①中两个结论仍然成立；
证明：如图2中，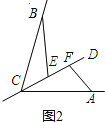
∵∠BEC=∠CFA=∠a，∠α+∠ACB=180°，
∴∠CBE=∠ACF，
在△BCE和△CAF中，
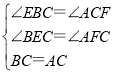
∴△BCE≌△CAF（AAS），
∴BE=CF，CE=AF，
∴EF=CF-CE=BE-AF，
当E在F的右侧时，同理可证EF=AF-BE，
∴EF=|BE-AF|；
故答案为∠α+∠ACB=180°．
（2）结论：EF=BE+AF．
理由：如图3中，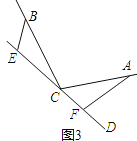
∵∠BEC=∠CFA=∠a，∠a=∠BCA，
又∵∠EBC+∠BCE+∠BEC=180°，∠BCE+∠ACF+∠ACB=180°，
∴∠EBC+∠BCE=∠BCE+∠ACF，
∴∠EBC=∠ACF，
在△BEC和△CFA中，
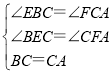
∴△BEC≌△CFA（AAS），
∴AF=CE，BE=CF，
∵EF=CE+CF，
∴EF=BE+AF．
