��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У������߹�ԭ��O������![]() �ύ����һ��
�ύ����һ��![]() ���䶥��Ϊ
���䶥��Ϊ![]() ������ͬѧ��һ�ѿ�Ϊ
������ͬѧ��һ�ѿ�Ϊ![]() ���̶ȵľ���ֱ�߶������߽������²�����
���̶ȵľ���ֱ�߶������߽������²�����
�� ����![]() ���� ��ֱ�ߵ�����������ߵĶԳ����غϣ�ʹ��ֱ�����¶˵��������ߵĶ����غϣ���ͼ1���������������ֱ���ұߵĽ���
���� ��ֱ�ߵ�����������ߵĶԳ����غϣ�ʹ��ֱ�����¶˵��������ߵĶ����غϣ���ͼ1���������������ֱ���ұߵĽ���![]() �Ŀ̶ȶ���Ϊ
�Ŀ̶ȶ���Ϊ![]() ��
��
������������⣺
��1��д�������ߵĶԳ��(2���������ߵĽ���ʽ����3����ͼ�е�ֱ�ߣ��㹻������ˮƽ��������ƽ�Ƶ���![]() ���ұߣ���ͼ2����ֱ�ߵ����߽�
���ұߣ���ͼ2����ֱ�ߵ����߽�![]() ���ڵ�
���ڵ�![]() ��
��![]() �����������ڵ�
�����������ڵ�![]() ��
��![]() ����֤��
����֤�� ![]() ��
��
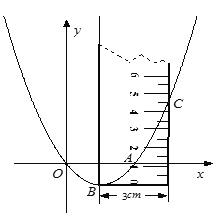
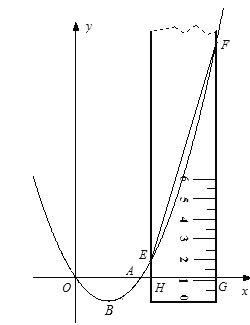
ͼ1 ͼ2
���𰸡���1��![]() ��2��
��2��![]() ��3��
��3��![]()
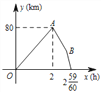
�������������������1������O��A���������߶Գ���Գƣ���OA=3cm���ɴ˿���������ߵĶԳ���Ϊx=![]() ��
��
��2������O��A�����꣬�ɽ������߽���ʽ��Ϊ����ʽ���ڣ�1��������������ߵĶԳ��ᣬ���ɵõ�B��C�ĺ����꣬�ֱ���������ߵĽ���ʽ�У���ʾ�����ǵ������꣬����C��B���������Ϊ4.5�����з����������ϵ����ֵ���Ӷ�ȷ�������ߵĽ���ʽ��
��3�������E��ĺ����꣬��������ֱ�ߵĿ��ȵõ�F��ĺ����꣬���ݣ�2�������������ߣ����ɱ�ʾ������������꣬�������ε������ʽ�����������EFGH���������ʽ��Ȼ��ͬ![]() ��EF2-9�����бȽϼ��ɣ�
��EF2-9�����бȽϼ��ɣ�
�����������1��![]()
��2���������ߵĽ���ʽΪ�� ![]() ����
����![]() ʱ��
ʱ�� ![]() ����
����![]() ����
����![]() ʱ��
ʱ�� ![]() ����
����![]() ��������ã�
��������ã� ![]() ����ã�
����ã� ![]() ��
��
�������ߵĽ���ʽΪ�� ![]() ��
��
��3������![]() ��
��![]() ������Ϊ
������Ϊ![]() ����
����![]() ��
�� ![]() ���ã�
���ã� ![]() ��
��
![]() ��
��
��![]() ����
���� ���ֱ����١��ڵã�
���ֱ����١��ڵã� ![]() ��
�� ![]()
��![]() �ã�
�ã� ![]()
��![]() ��
��![]()

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�