Question

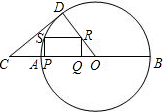如图，AB是⊙O的直径，C是BA延长线上的一点，CD与⊙O相切于点D，连接OD，四边形PQRS是矩形，其中点P、Q在半径OA上，点R在半径OD上，点S在⊙O上．已知CD=4，CO=5，PQ=2RQ，
（1）求

OQ

RQ

的值；
（2）求矩形PQRS的面积．

Answer 1

分析：（1）在Rt△ODC中，用勾股定理可求得⊙O的半径OD的长，易证得△ORQ∽△OCD，根据得到的比例线段即可求得OQ、RQ的比值．（利用∠DOC的余弦值求解亦可．）
（2）首先设出PQ的长，然后表示出OQ、PQ的值，连接OS，在Rt△OSP中，利用勾股定理易得RQ²的值，即可求得矩形PQRS的面积．

解答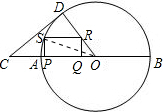：解：（1）因为CD与⊙O相切于点D，所以OD⊥CD．
在Rt△COD中，根据勾股定理，得
OD=

52-42

=3．（2分）
在△ORQ和△OCD中，因为∠OQR=∠ODC=90°，∠ROQ=∠COD，
所以Rt△ORQ∽Rt△OCD，（4分）
所以

OQ

OD

=

RQ

CD

，即

OQ

3

=

RQ

4

，所以

OQ

RQ

=

3

4

．（5分）
（用三角函数解，相应给分）

（2）连接OS．设RQ=x，则PQ=2x．由（1）知OQ=

3

4

x．
在Rt△OSP中，OP=PQ+OQ=2x+

3

4

x=

11

4

x．（7分）
根据勾股定理，得SP²+OP²=OS²，即x2+(

11

4

x)2=32，
解得x2=

144

137

，（9分）
所以2x2=

288

137

，即矩形PQRS的面积为

288

137

．

点评：此题考查的知识点有：切线的性质、相似三角形的判定和性质、勾股定理以及矩形面积的计算方法，难度适中．