题目内容
观察下列各式,并回答问题
1+3=4=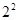
1+3+5=9=
1+3+5+7=16=
1+3+5+7+9=25=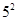
… …
(1)请你写出第10个式子;
(2)请你用含 n 的式子表示上述式子所表述的规律;
(3)计算1+3+5+7+9…+1003+1005+…+2009+2011;
(4)计算:1005+1007+……+2009+2011。
1+3=4=
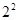
1+3+5=9=

1+3+5+7=16=

1+3+5+7+9=25=
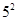
… …
(1)请你写出第10个式子;
(2)请你用含 n 的式子表示上述式子所表述的规律;
(3)计算1+3+5+7+9…+1003+1005+…+2009+2011;
(4)计算:1005+1007+……+2009+2011。
(1)112(2)(n+1)2(3)10062(4)760032
(1)1+3+5+7+9+11+13+15+17+19+21=121=112;
(2)1+3+5+7+9+…+2n+1=(n+1)2;
(3)1+3+5+7+9…+1003+1005+…+2009+2011=10062;
(4)原式=10062﹣5022=760032.
(1)由1+3=4=22,1+3+5=9=32,1+3+5+7=16=42,1+3+5+7+9=25=52,…可以看出连续奇数的和等于数的个数的平方;由此可以写出第10个式子;
(2)自然数n(n≥1)表示奇数为2n+1,因此得到一般规律;
(3)根据(2)中的规律可直接计算出结果;
(4)1005+1007+…+2009+2011=(1+3+5+…+2011)﹣(1+3+5+…+1003),再用(2)中的规律计算即可.
(2)1+3+5+7+9+…+2n+1=(n+1)2;
(3)1+3+5+7+9…+1003+1005+…+2009+2011=10062;
(4)原式=10062﹣5022=760032.
(1)由1+3=4=22,1+3+5=9=32,1+3+5+7=16=42,1+3+5+7+9=25=52,…可以看出连续奇数的和等于数的个数的平方;由此可以写出第10个式子;
(2)自然数n(n≥1)表示奇数为2n+1,因此得到一般规律;
(3)根据(2)中的规律可直接计算出结果;
(4)1005+1007+…+2009+2011=(1+3+5+…+2011)﹣(1+3+5+…+1003),再用(2)中的规律计算即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
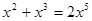 ②
②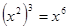 ③
③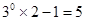
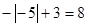 ⑤
⑤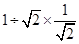 =1
=1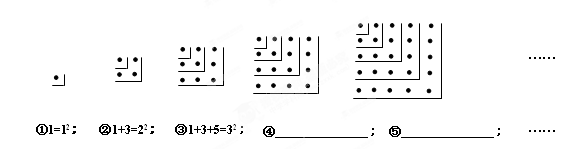
 的算术平方根是 ;-27的立方根是 .
的算术平方根是 ;-27的立方根是 .
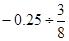
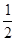
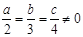 ,则
,则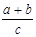 的值为( )
的值为( )