Question

【题目】如图,在△ABC中,D,E分别是AB,BC的中点.若△DBE的周长是6,则△ABC的周长是( )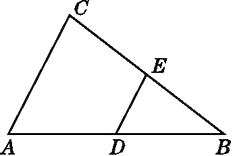
A.8
B.10
C.12
D.14

Answer 1

【答案】C
【解析】解：∵D,E分别是AB,BC的中点，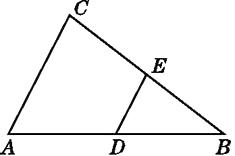
∴BE=BC，DB=AB，
DE是△ABC的中位线，
∴DE=AC
∴BE+DB+DE=（BC+AB+AC）
∵△DBE的周长是6，
∴BE+DB+DE=6
∴BC+AB+AC=2×6=12
∴△ABC的周长为12.
所以答案是：C
【考点精析】关于本题考查的线段的中点和三角形中位线定理，需要了解线段的中点到两端点的距离相等；连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半才能得出正确答案．