题目内容
某校数学研究小组在研究有关二次函数及其图象性质时,发现了一个重要结论:抛物线y=ax2+2x+3(a≠0),当实数a变化时,它们的顶点都在某条直线上.(1)请你协助探求出这条直线的表达式;
(2)问题(1)中的直线上有一个点不是该抛物线的顶点,你能找出它吗?并说明理由.
分析:(1)可以取a=1或-1,分别求出抛物线的顶点坐标,运用“两点法”求直线解析式;
(2)运用顶点坐标公式,先表示抛物线的顶点坐标,再根据a的取值范围进行判断.
(2)运用顶点坐标公式,先表示抛物线的顶点坐标,再根据a的取值范围进行判断.
解答:解:(1)当a=1时,y=x2+2x+3的顶点是(-1,2),
当a=-1时,y=-x2+2x+3的顶点是(1,4),
设直线的表达式为y=kx+b,则
,
解得
,
∴所求直线的表达式为y=x+3;
(2)抛物线y=ax2+2x+3的顶点是(-
,3-
),
而-
≠0,3-
≠3,
∴直线y=x+3一个点(0,3)不是该抛物线的顶点.
当a=-1时,y=-x2+2x+3的顶点是(1,4),
设直线的表达式为y=kx+b,则
|
解得
|
∴所求直线的表达式为y=x+3;
(2)抛物线y=ax2+2x+3的顶点是(-
| 1 |
| a |
| 1 |
| a |
而-
| 1 |
| a |
| 1 |
| a |
∴直线y=x+3一个点(0,3)不是该抛物线的顶点.
点评:本题考查了二次函数 的性质,待定系数法求一次函数解析式.关键是根据题意,采用特殊值法求直线解析式,根据顶点坐标的表达式求解.

练习册系列答案
相关题目
 ,纵坐标增加
,纵坐标增加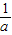 ,纵坐标增加
,纵坐标增加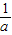 ,得到A点的坐标;若把顶点的横坐标增加
,得到A点的坐标;若把顶点的横坐标增加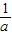 ,纵坐标增加
,纵坐标增加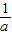 ,得到B点的坐标,则A、B两点一定仍在抛物线y=ax2+2x+3上.
,得到B点的坐标,则A、B两点一定仍在抛物线y=ax2+2x+3上.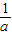 ,纵坐标增加
,纵坐标增加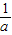 ,得到A点的坐标;若把顶点的横坐标增加
,得到A点的坐标;若把顶点的横坐标增加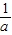 ,纵坐标增加
,纵坐标增加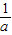 ,得到B点的坐标,则A、B两点一定仍在抛物线y=ax2+2x+3上.
,得到B点的坐标,则A、B两点一定仍在抛物线y=ax2+2x+3上.