题目内容
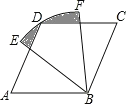
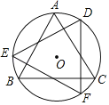
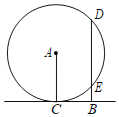
【题目】如图,直线BC与⊙A相切于点C,过B作CB的垂线交⊙O于D,E两点,已知AC=![]() ,CB=a,则以BE,BD的长为两根的一元二次方程是( )
,CB=a,则以BE,BD的长为两根的一元二次方程是( )
A.x2+bx+a2=0B.x2﹣bx+a2=0C.x2+bx﹣a2=0D.x2﹣bx﹣a2=0
【答案】B
【解析】
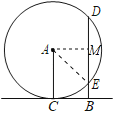
作AM⊥BD于M,连接AE,易得到AE=AC=![]() ,AM=CB=a,根据勾股定理求出DM=EM=
,AM=CB=a,根据勾股定理求出DM=EM=![]() ,进而求得BE+BD=b,BEBD=a2,则可确定一元二次方程.
,进而求得BE+BD=b,BEBD=a2,则可确定一元二次方程.
解:∵直线BC与⊙A相切于点C,
∴AC⊥BC,
作AM⊥BD于M,连接AE,
∴DM=EM,
∵BD⊥BC,
∴四边形ACBM是矩形,
∴BM=AC,AM=BC,
∵AE=AC=![]() ,AM=CB=a,
,AM=CB=a,
∴DM=EM=![]() ,
,
∴BE=BM﹣EM=![]() ﹣
﹣![]() ,BD=BM+DM=
,BD=BM+DM=![]() +
+![]() ,
,
∴BE+BD=b,BEBD=![]() ﹣(
﹣(![]() ﹣a2)=a2,
﹣a2)=a2,
∴以BE,BD的长为两根的一元二次方程是x2﹣bx+a2=0,
故选:B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】已知甲、乙两家公司员工日工资情况:甲公司日工资是底薪100元,每完成一件产品工资计3元;乙公司无底薪,40件以内(含40件)产品的部分每件产品工资计8元,超出40件的部分每件产品工资计10元,为此,在这两家公司各随机调查了100名工人日完成产品数,并整理得到如下频数分布表:
日完成产品数 | 38 | 39 | 40 | 41 | 42 |
甲公司工人数 | 20 | 40 | 20 | 10 | 10 |
乙公司工人数 | 10 | 20 | 20 | 40 | 10 |
(1)若甲、乙公司日工资加上其他福利,总的待遇相同,A、B两人分别到甲、乙公司应聘,都选中甲公司的概率是多少?
(2)试以这两家公司各100名工人日工资的平均数作为决策依据,若某人要去这两家公司应聘,为他做出选择,去哪一家公司的经济收入可能会多一些?