题目内容
已知，直角梯形的一条腰长为5cm这腰与底成30°的角，则这梯形的另一腰的长为（ ）
| A、10cm | B、5cm | C、2.5cm | D、7.5cm |
分析：过点A作AE∥CD交BC于点E，则四边形ADCE是平行四边形，则AE=CD=5，根据三角函数即可求得AB的长．
解答：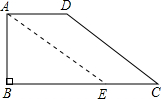
解：如图，在直角梯形ABCD中，∠B=90°，AD∥BC，∠C=30°，CD=5cm，
过点A作AE∥CD交BC于点E，则四边形ADCE是平行四边形，
有AE=CD=5，∠AEB=∠C=30°，
∴AB=AEsin30°=5×
=2.5cm
故选C．
解：如图，在直角梯形ABCD中，∠B=90°，AD∥BC，∠C=30°，CD=5cm，过点A作AE∥CD交BC于点E，则四边形ADCE是平行四边形，
有AE=CD=5，∠AEB=∠C=30°，
∴AB=AEsin30°=5×
| 1 |
| 2 |
故选C．
点评：本题通过作辅助线，把另一腰构造在一个直角三角形中，利用正弦的概念和平行四边形的性质求解．
练习册系列答案
相关题目