题目内容
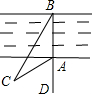 如图,小明为了测量河宽AB,先在BA延长线上取一点D,再在同岸取一点C,测得∠CAD=60°,∠BCA=30°,AC=15m,那么河AB宽为
如图,小明为了测量河宽AB,先在BA延长线上取一点D,再在同岸取一点C,测得∠CAD=60°,∠BCA=30°,AC=15m,那么河AB宽为
- A.15m
- B.
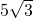 m
m - C.
 m
m - D.
 m
m
A
分析:先过C作CE⊥AB,在Rt△ACE中,根据∠CAD=60°,AC=15m可得出∠ACE的度数及AE、CE的长,再根据∠BCA=30°可求出∠BCE的度数,由锐角三角函数的定义即可得出BE的长,进而可求出AB的长.
解答: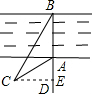 解:过C作CE⊥AB,
解:过C作CE⊥AB,
Rt△ACE中,
∵∠CAD=60°,AC=15m,
∴∠ACE=30°,AE= AC=
AC= ×15=7.5m,CE=AC•cos30°=15×
×15=7.5m,CE=AC•cos30°=15× =
=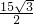 ,
,
∵∠BAC=30°,∠ACE=30°,
∴∠BCE=60°,
∴BE=CE•tan60°=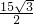 ×
× =22.5m,
=22.5m,
∴AB=BE-AE=22.5-7.5=15m.
故选A.
点评:本题考查的是解直角三角形的应用-方向角问题,解答此题的关键是作出辅助线构造出直角三角形,利用三角形内角和定理及直角三角形的性质进行解答.
分析:先过C作CE⊥AB,在Rt△ACE中,根据∠CAD=60°,AC=15m可得出∠ACE的度数及AE、CE的长,再根据∠BCA=30°可求出∠BCE的度数,由锐角三角函数的定义即可得出BE的长,进而可求出AB的长.
解答:
 解:过C作CE⊥AB,
解:过C作CE⊥AB,Rt△ACE中,
∵∠CAD=60°,AC=15m,
∴∠ACE=30°,AE=
 AC=
AC= ×15=7.5m,CE=AC•cos30°=15×
×15=7.5m,CE=AC•cos30°=15× =
=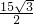 ,
,∵∠BAC=30°,∠ACE=30°,
∴∠BCE=60°,
∴BE=CE•tan60°=
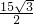 ×
× =22.5m,
=22.5m,∴AB=BE-AE=22.5-7.5=15m.
故选A.
点评:本题考查的是解直角三角形的应用-方向角问题,解答此题的关键是作出辅助线构造出直角三角形,利用三角形内角和定理及直角三角形的性质进行解答.

练习册系列答案
相关题目
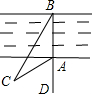 如图,小明为了测量河宽AB,先在BA延长线上取一点D,再在同岸取一点C,测得∠CAD=60°,∠BCA=30°,AC=15m,那么河AB宽为( )
如图,小明为了测量河宽AB,先在BA延长线上取一点D,再在同岸取一点C,测得∠CAD=60°,∠BCA=30°,AC=15m,那么河AB宽为( )| A、15m | ||
B、5
| ||
C、10
| ||
D、12
|
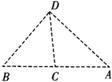 18、如图,小明为了测量河的宽度,他站在河边的点C,头顶为点D,面向河对岸,压低帽檐使目光正好落在河对岸的岸边点A,然后他姿势不变,在原地方转了180°,正好看见了他所在的岸上的一块石头点B,他测出BC=30m,你能猜出河有多宽吗?说说理由.答:
18、如图,小明为了测量河的宽度,他站在河边的点C,头顶为点D,面向河对岸,压低帽檐使目光正好落在河对岸的岸边点A,然后他姿势不变,在原地方转了180°,正好看见了他所在的岸上的一块石头点B,他测出BC=30m,你能猜出河有多宽吗?说说理由.答: