题目内容
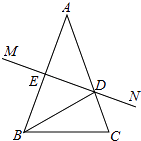
【题目】如图a,在平面直角坐标系中,A、B坐标分别为(6,0),(0,6),P为线段AB上的一点.
(1) 如图a,若三角形OAP的面积是12,求点P的坐标;
(2)如图b,若P为AB的中点,点M,N分别是OA,OB边上的动点,点M从顶点A,点N从顶点O同时出发,且它们的速度都为1cm/s,则在M,N运动的过程中,线段PM,PN之间有何关系?并证明;
(3)如图c,若P为线段AB上异于A,B的任意一点,过B点作BD⊥OP,交OP,OA分别于F,D两点,E为OA上一点,且∠PEA=∠BDO,试判断线段OD与AE的数量关系,并说明理由.

【答案】(1)P(2,4);(2)PM=PN,且PM⊥PN,证明见解析;(3)OD=AE,理由见解析.
【解析】试题分析:(1)根据点的坐标以及三角形的面积即可求得;
(2)连接OP,证明△NOP≌△MAP,根据全等三角形的对应边相等、对应角相等可得PN=PM,∠OPN=∠APM,从而可得PM与PN的位置关系;
(3)作AQ⊥AO 交OP延长线于Q,证明△OBD≌△AOQ,△APE≌△APQ,从而即可得.
试题解析:(1)∵A(6,0),B(0,6),∴OA=OB=6,
∴S△AOB=18,
设P的坐标为(xP,yP),
∵![]() =12,
=12,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴P(2,4);
(2)PM=PN 且PM⊥PN,
证明如下:
如图1,连接PO,

在△NOP和△MAP中,
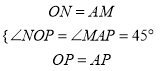 ,
,
∴△NOP≌△MAP,
∴ PN=PM,
且∠OPN=∠APM,
又∵∠APM+∠MPO=90° ,
∴∠OPN+∠MPO=90° ,即∠MPN=90° ,
∴PM⊥PN,
综上:PM=PN 且PM⊥PN;
(3)OD=AE,理由:如图2,
作AQ⊥AO 交OP延长线于Q,
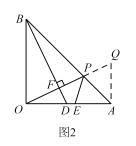
易知∠OBD=∠AOQ,
在△OBD和△AOQ中,
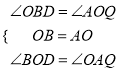 ,
,
∴△OBD≌△AOQ,
∴∠BDO=∠Q=∠PEA,OD=AQ,
易证△APE≌△APQ,
∴ AE=AQ=OD,
∴ OD=AE.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】甲、乙两城市为了解决空气质量污染问题,对城市及其周边的环境污染进行了综合治理.在治理过程中,环保部门每月初对两个城市的空气质量进行监测,连续10个月的空气污染指数如下图所示.其中,空气污染指≤50时,空气质量为优;50<空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻微污染.

(1)请填写下表:
平均数 | 方差 | 中位数 | 空气质量为优的次数 | |
甲 | 80 | 1 | ||
乙 | 1060 | 80 |
(2)请回答下面问题:
①从平均数和中位数来分析,甲、乙两个城市的空气质量;
②从平均数和方差来分析,甲、乙两个城市的空气质量变化情况;
③根据折线图上两城市的空气污染指数的走势及优的情况来分析两城市治理环境污染的效果.