题目内容
如图,函数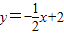 的图象交y轴于M,交x轴于N,点P是直线MN上任意一点,PQ⊥x轴,Q是垂足,设点Q的坐标为(t,0),△POQ的面积为S(当点P与M、N重合时,其面积记为0).
的图象交y轴于M,交x轴于N,点P是直线MN上任意一点,PQ⊥x轴,Q是垂足,设点Q的坐标为(t,0),△POQ的面积为S(当点P与M、N重合时,其面积记为0).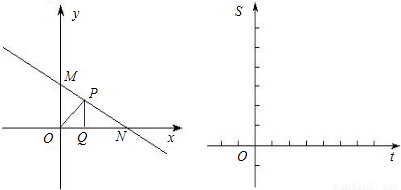
(1)试求S与t之间的函数关系式;
(2)在如图所示的直角坐标系内画出这个函数的图象,并利用图象求使得S=a(a>0)的点P的个数.
【答案】分析:本题要根据题意把各种情况都讨论出来,同时把△POQ的面积表示出来.(2)要根据题意列式整理分析,在根据解析式画出图象.
解答: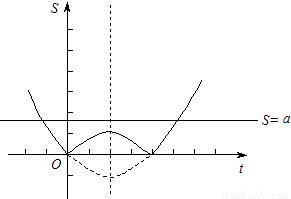 解:
解:
解法1:(1)①当t<0时,OQ=-t,PQ=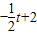 ,
,
∴S=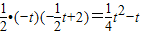 ;
;
②当0<t<4时,OQ=t,PQ=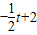 ,
,
∴S=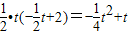 ;
;
③当t>4时,OQ=t,PQ=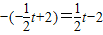 ,
,
∴S=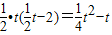 ;
;
④当t=0或4时,S=0;
于是,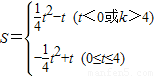 (6分)
(6分)
(2)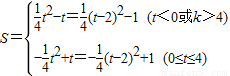
下图中的实线部分就是所画的函数图象.(12分)
观察图象可知:
当0<a<1时,符合条件的点P有四个;
当a=1时,符合条件的点P有三个;
当a>1时,符合条件的点P只有两个.(15分)
解法2:(1)∵OQ=|t|,PQ=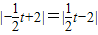 ,
,
∴S=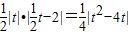 (4分)
(4分)
(2)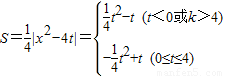 (6分)
(6分)
以下同解法1.
点评:本题考查一次函数有关分情况讨论的问题,解题中要注意对各种情况做出准确分析,尤其是t值做好取值范围的分段,
解答:
 解:
解:解法1:(1)①当t<0时,OQ=-t,PQ=
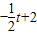 ,
,∴S=
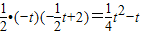 ;
;②当0<t<4时,OQ=t,PQ=
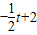 ,
,∴S=
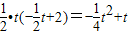 ;
;③当t>4时,OQ=t,PQ=
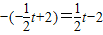 ,
,∴S=
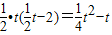 ;
;④当t=0或4时,S=0;
于是,
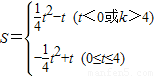 (6分)
(6分)(2)
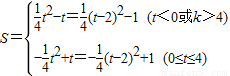
下图中的实线部分就是所画的函数图象.(12分)
观察图象可知:
当0<a<1时,符合条件的点P有四个;
当a=1时,符合条件的点P有三个;
当a>1时,符合条件的点P只有两个.(15分)
解法2:(1)∵OQ=|t|,PQ=
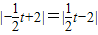 ,
,∴S=
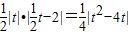 (4分)
(4分)(2)
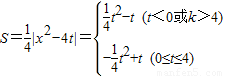 (6分)
(6分)以下同解法1.
点评:本题考查一次函数有关分情况讨论的问题,解题中要注意对各种情况做出准确分析,尤其是t值做好取值范围的分段,

练习册系列答案
相关题目
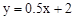 的图象与x轴交于点A,与二次函数
的图象与x轴交于点A,与二次函数 的图象交于y轴上的一点B,二次函数
的图象交于y轴上的一点B,二次函数
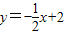 的图象交y轴于M,交x轴于N,点P是直线MN上任意一点,PQ⊥x轴,Q是垂足,设点Q的坐标为(t,0),△POQ的面积为S(当点P与M、N重合时,其面积记为0).
的图象交y轴于M,交x轴于N,点P是直线MN上任意一点,PQ⊥x轴,Q是垂足,设点Q的坐标为(t,0),△POQ的面积为S(当点P与M、N重合时,其面积记为0).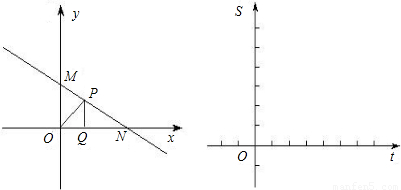
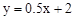 的图象与x轴交于点A,与二次函数
的图象与x轴交于点A,与二次函数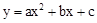 的图象交于y轴上的一点B,二次函数
的图象交于y轴上的一点B,二次函数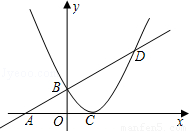
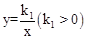 和
和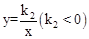 。点A在y轴的正半轴上,过点A作直线BC∥x轴,且分别与两个反比例函数的图象交于点B和C,连接OC、OB。若△BOC的面积为
。点A在y轴的正半轴上,过点A作直线BC∥x轴,且分别与两个反比例函数的图象交于点B和C,连接OC、OB。若△BOC的面积为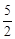 ,AC:AB=2:3,则
,AC:AB=2:3,则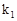 = ▲ ,
= ▲ ,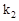 = ▲ 。
= ▲ 。