题目内容
反比例函数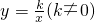 的图象上有一点P(m,n),且m,n是一元二次方程x2-4x+3=0的两根,则k=________.
的图象上有一点P(m,n),且m,n是一元二次方程x2-4x+3=0的两根,则k=________.
3
分析:用因式分解求出方程的两个根,得到p点的坐标,代入反比例函数求出k的值.
解答:(x-1)(x-3)=0,
∴x-1=0或x-3=0,
解得x1=1,x2=3.
∴p(1,3)或(3,1)
∵点p在反比例函数的图象上,
∴k=1×3=3.
故答案是:3.
点评:本题考查的是用因式分解法解一元二次方程,求出方程的根后,再根据反比例函数图象上点的特征求出k的值.
分析:用因式分解求出方程的两个根,得到p点的坐标,代入反比例函数求出k的值.
解答:(x-1)(x-3)=0,
∴x-1=0或x-3=0,
解得x1=1,x2=3.
∴p(1,3)或(3,1)
∵点p在反比例函数的图象上,
∴k=1×3=3.
故答案是:3.
点评:本题考查的是用因式分解法解一元二次方程,求出方程的根后,再根据反比例函数图象上点的特征求出k的值.

练习册系列答案
相关题目
已知反比例函数的图象上有一点A(-2,1),则下列各点中一定在此反比例函数图象上的是( )
| A、(1,2) | ||
| B、(1,-2) | ||
| C、(-1,-2) | ||
D、(
|
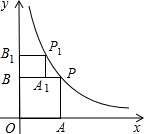 如图,已知反比例函数
如图,已知反比例函数