题目内容
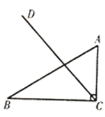
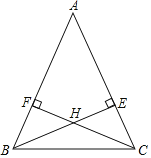
【题目】如图,AB=AC,BE与CF是△ABC的高线,且BE与CF相交于点H.
(1)求证:HB=HC;
(2)不添加辅助线,直接写出图中所有的全等三角形.
【答案】(1)证明见解析;(2)全等三角形有△AEB≌△AFC,△BEC≌△CFB,△BFH≌△CEH.
【解析】
(1)根据高求出∠BEC=∠BFC=90°,根据等腰三角形的性质得出∠ABC=∠ACB,根据三角形内角和定理求∠EBC=∠BCF,根据等腰三角形的判定得出即可;
(2)根据全等三角形的判定逐个判断即可.
解:(1)∵BE与CF是△ABC的高线,
∴∠BEC=∠BFC=90°,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠BEC+∠ACB+∠EBC=180°,∠CFB+∠ABC+∠BCF=180°,
∴∠EBC=∠BCF,
∴HB=HC;
(2)解:由(1)可知:AB=AC, ∠BEC=∠BFC=90°, ∠ABC=∠ACB,∠EBC=∠BCF
∴利用ASA定理可以判定△AEB≌△AFC;
利用AAS定理可以判定△BEC≌△CFB;△BFH≌△CEH,
∴全等三角形有△AEB≌△AFC,△BEC≌△CFB,△BFH≌△CEH.

练习册系列答案
相关题目