题目内容
将一根15厘米长的吸管（无弯折）放进高为12厘米，底面圆直径为5厘米的圆柱形玻璃杯中，露出杯口的长度为x厘米，则x的取值范围是
2cm≤x≤3cm
2cm≤x≤3cm
．分析：根据题意构建直角三角形，利用勾股定理即可解答．
解答：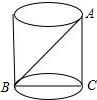
解：如图，由题意可知BC=5cm，AC=12cm，
由勾股定理得AB=
=13cm．
当木棒垂直于地面时露在杯子外面的部分长度最长为，15-AC=15-12=3cm，
当木棒与AB重合时露在杯子外面的部分长度最短为15-AB=15-13=2cm，
故棒露在杯子外面的部分长度x的范围是2cm≤x≤3cm，
故答案为：2cm≤x≤3cm．
解：如图，由题意可知BC=5cm，AC=12cm，由勾股定理得AB=
| AC2 +BC2 |
当木棒垂直于地面时露在杯子外面的部分长度最长为，15-AC=15-12=3cm，
当木棒与AB重合时露在杯子外面的部分长度最短为15-AB=15-13=2cm，
故棒露在杯子外面的部分长度x的范围是2cm≤x≤3cm，
故答案为：2cm≤x≤3cm．
点评：本题考查正确运用勾股定理，善于观察题目的信息是解题以及学好数学的关键．
练习册系列答案
相关题目