题目内容
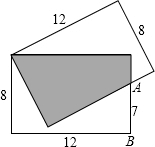如图，让两个长为12，宽为8的矩形重叠，已知AB长为7，则两个矩形重叠的阴影部分面积为（ ）| A、36 | B、42 | C、48 | D、56 |
分析：首先作图，连接AC，根据题干条件求出CD=8，CE=12，AE=8-7=1，然后根据三角形面积公式求出S△AEC和S△ACD，即阴影部分的面积．
解答：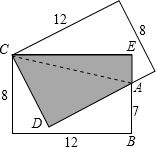
解：如图，连接AC，
CD=8，CE=12，AE=8-7=1，
Rt△ACE中，AC=
=
，
Rt△ADC中，AD=
=9，
阴影部分的面积=S△AEC+S△ACD=CD×AD÷2+AE×CD÷2=42．
故选B．
解：如图，连接AC，CD=8，CE=12，AE=8-7=1，
Rt△ACE中，AC=
| AE2+CE2 |
| 145 |
Rt△ADC中，AD=
| AC2-CD2 |
阴影部分的面积=S△AEC+S△ACD=CD×AD÷2+AE×CD÷2=42．
故选B．
点评：本题考查了矩形的性质和直角三角形中勾股定理的运用，此题难度不大，但是要看出阴影面积=S△AEC+S△ACD．
练习册系列答案
开心练习课课练与单元检测系列答案
开心试卷期末冲刺100分系列答案
相关题目
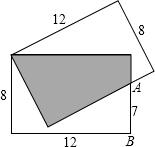如图，让两个长为12，宽为8的矩形重叠，已知图中线段AB长为7，则两个矩形重叠的阴影部分面积为
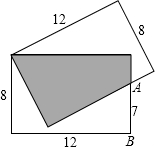如图，让两个长为12，宽为8的矩形重叠，已知图中线段AB长为7，则两个矩形重叠的阴影部分面积为________．
