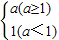题目内容
阅读下列材料:已知三个数a、b、c,我们可以用M(a,b,c)表示这三个数的平均数,用max(a,b,c)表示这三个数中最大的数.
例如:M(-2,1,5)=
| -2+1+5 |
| 3 |
| 4 |
| 3 |
|
解决下列问题:
(1)填空:①M(-3,-2,10)=
②max(tan30°,sin45°,cos60°)=
③如果max(2,2-2a,2a-4)=2,那么a的取值范围是
(2)如果M(2,a+1,2a)=max(2,a+1,2a),求a的值;
(3)请你根据(2)的结果,继续探究:如果M(a,b,c)=max(a,b,c),那么
(4)运用(3)的结论填空:
如果M(2a+b+2,a+2b,2a-b)=max(2a+b+2,a+2b,2a-b),那么a+b=
分析:(1)由给出的平均数和最大数进行填空即可;
(2)分两种情况列出等式,求得a的值即可;
(3)不妨假设max(a,b,c)=a,可证得a=b=c;
(4)列式求得a、b,再代入a+b即可.
(2)分两种情况列出等式,求得a的值即可;
(3)不妨假设max(a,b,c)=a,可证得a=b=c;
(4)列式求得a、b,再代入a+b即可.
解答:解:(1)①
;
②
(填sin45°也正确);
③0≤a≤3
(2)当M(2,a+1,2a)=
=a+1=max(2,a+1,2a)
∴
解得:a=1
(3)a=b=c
证明:M(a,b,c)=
不妨假设max(a,b,c)=a那么
∴a-b≥0且a-c≥0,
∵M(a,b,c)=max(a,b,c),
∴
=a
∴2a-b-c=0,
∴a=ba=c,即a=b=c(其它两种情况同理)
(4)-4
| 5 |
| 3 |
②
| ||
| 2 |
③0≤a≤3
(2)当M(2,a+1,2a)=
| 2+a+1+2a |
| 3 |
∴
|
(3)a=b=c
证明:M(a,b,c)=
| a+b+c |
| 3 |
|
∴a-b≥0且a-c≥0,
∵M(a,b,c)=max(a,b,c),
∴
| a+b+c |
| 3 |
∴2a-b-c=0,
∴a=ba=c,即a=b=c(其它两种情况同理)
(4)-4
点评:本题是一个新定义的题目,考查了一元一次不等式的应用和特殊角的三角函数值,难度较大.

练习册系列答案
相关题目


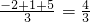 ; max(-2,1,5)=5;max(-2,1,a)=
; max(-2,1,5)=5;max(-2,1,a)=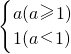
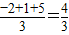 ; max(-2,1,5)=5;max(-2,1,a)=
; max(-2,1,5)=5;max(-2,1,a)=