题目内容
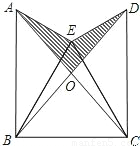
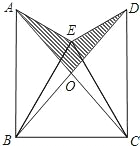 如图,已知△BEC是等边三角形,∠AEB=∠DEC=90°,AE=DE,AC,BD的交点为O.
如图,已知△BEC是等边三角形,∠AEB=∠DEC=90°,AE=DE,AC,BD的交点为O.(1)求证:△AEC≌△DEB;
(2)若∠ABC=∠DCB=90°,AB=2 cm,求图中阴影部分的面积.
分析:(1)在△AEB和△DEC中,已知AE=DE,BE=CE,且夹角相等,根据边角边可证全等.
(2)由图可知,在连接EO并延长EO交BC于点F,连接AD之后,整个图形是一个以EF所在直线对称的图形.即△AEO和△DEO面积相等,只要求出其中一个即可,而三角形AEO面积=
•OE•FB,所以解题中心即为求出OE和FB,有(1)中结论和已知条件即可求解.
(2)由图可知,在连接EO并延长EO交BC于点F,连接AD之后,整个图形是一个以EF所在直线对称的图形.即△AEO和△DEO面积相等,只要求出其中一个即可,而三角形AEO面积=
| 1 |
| 2 |
解答: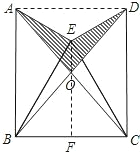 (1)证明:∵∠AEB=∠DEC=90°,
(1)证明:∵∠AEB=∠DEC=90°,
∴∠AEB+∠BEC=∠DEC+∠BEC,即∠AEC=∠DEB,
∵△BEC是等边三角形,
∴CE=BE,
又AE=DE,
∴△AEC≌△DEB.
(2)解:连接EO并延长EO交BC于点F,连接AD.由(1)知AC=BD.
∵∠ABC=∠DCB=90°,∴∠ABC+∠DCB=180°,
∴AB∥DC,AB=
=
=CD,
∴四边形ABCD为平行四边形且是矩形,
∴OA=OB=OC=OD,
又∵BE=CE,
∴OE所在直线垂直平分线段BC,
∴BF=FC,∠EFB=90°.
∴OF=
AB=
×2=1,
∵△BEC是等边三角形,
∴∠EBC=60°.
在Rt△AEB中,∠AEB=90°,
∠ABE=∠ABC-∠EBC=90°-60°=30°,
∴BE=AB•cos30°=2×
=
,
在Rt△BFE中,∠BFE=90°,∠EBF=60°,
∴BF=BE•cos60°=
×
=
,
EF=BE•sin60°=
×
=
,
∴OE=EF-OF=
-1=
,
∵AE=ED,OE=OE,AO=DO,
∴△AOE≌△DOE.∴S△AOE=S△DOE
∴S阴影=2S△AOE=2×
•EO•BF=2×
×
×
=
(cm2).
 (1)证明:∵∠AEB=∠DEC=90°,
(1)证明:∵∠AEB=∠DEC=90°,∴∠AEB+∠BEC=∠DEC+∠BEC,即∠AEC=∠DEB,
∵△BEC是等边三角形,
∴CE=BE,
又AE=DE,
∴△AEC≌△DEB.
(2)解:连接EO并延长EO交BC于点F,连接AD.由(1)知AC=BD.
∵∠ABC=∠DCB=90°,∴∠ABC+∠DCB=180°,
∴AB∥DC,AB=
| AC2-BC2 |
| BD2-BC2 |
∴四边形ABCD为平行四边形且是矩形,
∴OA=OB=OC=OD,
又∵BE=CE,
∴OE所在直线垂直平分线段BC,
∴BF=FC,∠EFB=90°.
∴OF=
| 1 |
| 2 |
| 1 |
| 2 |
∵△BEC是等边三角形,
∴∠EBC=60°.
在Rt△AEB中,∠AEB=90°,
∠ABE=∠ABC-∠EBC=90°-60°=30°,
∴BE=AB•cos30°=2×
| ||
| 2 |
| 3 |
在Rt△BFE中,∠BFE=90°,∠EBF=60°,
∴BF=BE•cos60°=
| 3 |
| 1 |
| 2 |
| ||
| 2 |
EF=BE•sin60°=
| 3 |
| ||
| 2 |
| 3 |
| 2 |
∴OE=EF-OF=
| 3 |
| 2 |
| 1 |
| 2 |
∵AE=ED,OE=OE,AO=DO,
∴△AOE≌△DOE.∴S△AOE=S△DOE
∴S阴影=2S△AOE=2×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
点评:考查综合应用等边三角形、等腰三角形、解直角三角形、直角三角形性质,进行逻辑推理能力和运算能力.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
 如图,已知△BEC是等边三角形,∠AEB=∠DEC=90°,AE=DE,AC,BD的交点为O.
如图,已知△BEC是等边三角形,∠AEB=∠DEC=90°,AE=DE,AC,BD的交点为O.
(1)求证:△AEC≌△DEB;
(2)若∠ABC=∠DCB=90°,AB=2 cm,求图中阴影部分的面积.
如图,已知△BEC是等边三角形,∠AEB=∠DEC=90°,AE=DE,AC,BD的交点为O.
(1)求证:△AEC≌△DEB;
(2)若∠ABC=∠DCB=90°,AB=2 cm,求图中阴影部分的面积.

(1)求证:△AEC≌△DEB;
(2)若∠ABC=∠DCB=90°,AB=2 cm,求图中阴影部分的面积.