题目内容
如图所示,抛物线y=mx2+8mx+12n与x轴交于A、B两点(点A在点B的左边),在第二象限内 抛物线上的一点C,使△OCA∽△OBC,且AC:BC=
抛物线上的一点C,使△OCA∽△OBC,且AC:BC=| 3 |
(1)当C恰为AP中点时,求抛物线和直线AP的解析式;
(2)若点M在抛物线的对称轴上,⊙M与直线PA和y轴都相切,求点M的坐标.
分析:(1)设出抛物线y=mx2+8mx+12n与x轴交于A、B两点的坐标,利用△OCA∽△OBC,证得△ABC为直角三角形,进一步求得P点坐标,利用待定系数法求得直线解析式;
(2)利用抛物线的对称性,首先抛物线解析式及双切线的性质求得点M横坐标,再进一步利用三角形全等的性质和(1)所求直线解决问题.
(2)利用抛物线的对称性,首先抛物线解析式及双切线的性质求得点M横坐标,再进一步利用三角形全等的性质和(1)所求直线解决问题.
解答:解:(1)设y=mx2+8mx+12n与x轴交于A、B两点,A(x1,0)、B(x2,0),
在Rt△APO中,
∵C为AP中点,
∴OC=
AP=AC=CP,
∵△OCA∽△OBC,
∴
=
=
=
.
设AC=
k,BC=k,OA?OB=OC2=3k2,
∴OC=
k,PC=
k,OB=k,OA=3k,AB=2k,OP=
k.
在△ABC中,
∵BC2+AC2=AB2,
∴∠ACB=90°,∠CAB=30°.
∵x1+x2=-BO-AO=-(AO+BO)=-
=-8,
∴-k-3k=-4k=-8,
∴k=2.
∴A(-6,0),B(-2,0),
∴OP=2
,P(0,2
).
设AP直线y=knx+2
,A(-6,0)代入得0=-6kn+2
,
∴kn=
,直线AP为y=
x+2
;
(2)如图,
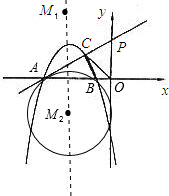 设抛物线的对称轴为M1M2,由题意M1到y轴距离M1P1=M1N1(N1为M1N1⊥AP的垂足).
设抛物线的对称轴为M1M2,由题意M1到y轴距离M1P1=M1N1(N1为M1N1⊥AP的垂足).
同理M2P2=M2N2.
∵y=-
x2-
x-4
,
∴-
=-4
∴M1和M2的横坐标均为-4.
设M1M2与AP交于Q点,M1N1=M2N2=4=M1P1=M2P2=4,
∵OP=
k,AP=2
k,
∴∠PAO=30°,∠AQM2=60°,
将Q点横坐标-4代入直线AP方程:y=
×(-4)+2
=-
+
=
;
∵△M1QN1≌△M2QN2,
∴M1Q=M2Q=
×2=
.
∴M1的纵坐标=
+
=
,
∴M1(-4,
).
∴M2点的纵坐标为(
-
)=
=2
的相反数-2
,
∴M2(-4,-2
).
综上,抛物线:y=-
x2-
x-4
,直线AP:y=
x+2
,M1(-4,
),M2(-4,-2
).
在Rt△APO中,
∵C为AP中点,
∴OC=
| 1 |
| 2 |
∵△OCA∽△OBC,
∴
| OC |
| OB |
| OA |
| OC |
| AC |
| BC |
| 3 |
设AC=
| 3 |
∴OC=
| 3 |
| 3 |
| 3 |
在△ABC中,
∵BC2+AC2=AB2,
∴∠ACB=90°,∠CAB=30°.
∵x1+x2=-BO-AO=-(AO+BO)=-
| 8m |
| m |
∴-k-3k=-4k=-8,
∴k=2.
∴A(-6,0),B(-2,0),
∴OP=2
| 3 |
| 3 |
设AP直线y=knx+2
| 3 |
| 3 |
∴kn=
| ||
| 3 |
| ||
| 3 |
| 3 |
(2)如图,
 设抛物线的对称轴为M1M2,由题意M1到y轴距离M1P1=M1N1(N1为M1N1⊥AP的垂足).
设抛物线的对称轴为M1M2,由题意M1到y轴距离M1P1=M1N1(N1为M1N1⊥AP的垂足).同理M2P2=M2N2.
∵y=-
| ||
| 3 |
8
| ||
| 3 |
| 3 |
∴-
| b |
| 2a |
∴M1和M2的横坐标均为-4.
设M1M2与AP交于Q点,M1N1=M2N2=4=M1P1=M2P2=4,
∵OP=
| 3 |
| 3 |
∴∠PAO=30°,∠AQM2=60°,
将Q点横坐标-4代入直线AP方程:y=
| ||
| 3 |
| 3 |
4
| ||
| 3 |
6
| ||
| 3 |
2
| ||
| 3 |
∵△M1QN1≌△M2QN2,
∴M1Q=M2Q=
| 4 | ||
|
8
| ||
| 3 |
∴M1的纵坐标=
8
| ||
| 3 |
2
| ||
| 3 |
10
| ||
| 3 |
∴M1(-4,
10
| ||
| 3 |
∴M2点的纵坐标为(
8
| ||
| 3 |
2
| ||
| 3 |
6
| ||
| 3 |
| 3 |
| 3 |
∴M2(-4,-2
| 3 |
综上,抛物线:y=-
| ||
| 3 |
8
| ||
| 3 |
| 3 |
| ||
| 3 |
| 3 |
10
| ||
| 3 |
| 3 |
点评:此题考查待定系数法求函数解析式,三角形相似的性质,二次函数的对称性,双切线的性质解决问题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
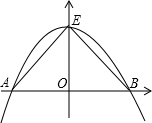 如图所示,抛物线y=ax2+bx+c与两坐标轴的交点分别是A、B、E,且△ABE是等腰直角三角形,AE=BE,则下列关系式中不能成立的是( )
如图所示,抛物线y=ax2+bx+c与两坐标轴的交点分别是A、B、E,且△ABE是等腰直角三角形,AE=BE,则下列关系式中不能成立的是( )| A、b=0 | B、S△ABE=c2 | C、ac=-1 | D、a+c=0 |
 (2012•河源二模)已知:如图所示,抛物线y=-x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0).
(2012•河源二模)已知:如图所示,抛物线y=-x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0). (2012•槐荫区一模)如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(-1,0)、(0,-3).
(2012•槐荫区一模)如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(-1,0)、(0,-3).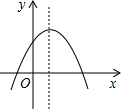 (1997•陕西)如图所示,抛物线对应的函数解析表达式只可能是( )
(1997•陕西)如图所示,抛物线对应的函数解析表达式只可能是( ) (1997•陕西)如图所示的抛物线是把y=-x2经过平移而得到的.这时抛物线过原点O和x轴正向上一点A,顶点为P;
(1997•陕西)如图所示的抛物线是把y=-x2经过平移而得到的.这时抛物线过原点O和x轴正向上一点A,顶点为P;