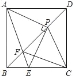
题目内容
【题目】如图,P是边长为1的正方形ABCD对角线BD上一动点(P与B、D不重合),∠APE=90°,且点E在BC边上,AE交BD于点F.
(1)求证:①△PAB≌△PCB;②PE=PC;
(2)在点P的运动过程中,![]() 的值是否改变?若不变,求出它的值;若改变,请说明理由;
的值是否改变?若不变,求出它的值;若改变,请说明理由;
(3)设DP=x,当x为何值时,AE∥PC,并判断此时四边形PAFC的形状.
【答案】(1)见解析;
(2)![]() ;
;
(3)x=![]() ﹣1;四边形PAFC是菱形.
﹣1;四边形PAFC是菱形.
【解析】
试题分析:(1)根据四边形ABCD是正方形,得出AB=BC,∠ABP=∠CBP°,再根据PB=PB,即可证出△PAB≌△PCB,
②根据∠PAB+∠PEB=180°,∠PEC+∠PEB=180°,得出∠PEC=∠PCB,从而证出PE=PC;
(2)根据PA=PC,PE=PC,得出PA=PE,再根据∠APE=90°,得出∠PAE=∠PEA=45°,即可求出![]() ;
;
(3)先求出∠CPE=∠PEA=45°,从而得出∠PCE,再求出∠BPC即可得出∠BPC=∠PCE,从而证出BP=BC=1,x=![]() ﹣1,再根据AE∥PC,得出∠AFP=∠BPC=67.5°,由△PAB≌△PCB得出∠BPA=∠BPC=67.5°,PA=PC,从而证出AF=AP=PC,得出答案.
﹣1,再根据AE∥PC,得出∠AFP=∠BPC=67.5°,由△PAB≌△PCB得出∠BPA=∠BPC=67.5°,PA=PC,从而证出AF=AP=PC,得出答案.
试题解析:(1)①∵四边形ABCD是正方形,∴AB=BC,∠ABP=∠CBP=![]() ∠ABC=45°.
∠ABC=45°.
∵PB=PB,∴△PAB≌△PCB (SAS).
②由△PAB≌△PCB可知,∠PAB=∠PCB.∵∠ABE=∠APE=90°,∴∠PAB+∠PEB=180°,
又∵∠PEC+∠PEB=180°,∴∠PEC=∠PAB=∠PCB,∴PE=PC.
(2)在点P的运动过程中,![]() 的值不改变.
的值不改变.
由△PAB≌△PCB可知,PA=PC.
∵PE=PC,
∴PA=PE,
又∵∠APE=90°,
∴△PAE是等腰直角三角形,∠PAE=∠PEA=45°,∴![]() =
=![]() .
.
(3)∵AE∥PC,∴∠CPE=∠PEA=45°,∴在△PEC中,∠PCE=∠PEC=![]() (180°﹣45°)=67.5°.
(180°﹣45°)=67.5°.
在△PBC中,∠BPC=(180°﹣∠CBP﹣∠PCE)=(180°﹣45°﹣67.5°)=67.5°.
∴∠BPC=∠PCE=67.5°,∴BP=BC=1,∴x=BD﹣BP=![]() ﹣1.∵AE∥PC,
﹣1.∵AE∥PC,
∴∠AFP=∠BPC=67.5°,由△PAB≌△PCB可知,∠BPA=∠BPC=67.5°,PA=PC,
∴∠AFP=∠BPA,∴AF=AP=PC,∴四边形PAFC是菱形.

