题目内容
已知:一条抛物线的开口向上,顶点为A(-2,0),与y轴相交于点B,过点B作BC∥x轴,交抛物线于点C,过点C作CD∥AB,交x轴于点D.
(1)求点D的坐标.
(2)试探索:AC与BD能否互相垂直?如果能,请求出以这条抛物线为图象的二次函数的解析式;如果不能,请说明理由.
解:(1)根据题意,得点B、C关于直线x=-2对称,点B的横坐标为0,
∴点C的横坐标为-4.
∴BC=4.
∵BC∥AD,CD∥AB,
∴四边形ABCD是平行四边形.
∴AD=4.
∴点D的坐标为(-6,0).
(2)能.
要使AC与BD互相垂直,必须使平行四边形ABCD是菱形,
即AB=BC=4.
∵AO=2,∴ ,即点B的坐标为(0,
,即点B的坐标为(0, ).
).
设所求的二次函数的解析式为y=a(x+2)2.
代入点B的坐标,得 .
.
∴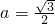 .
.
∴当二次函数的解析式为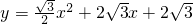 时,AC⊥BD.
时,AC⊥BD.
分析:(1)本题需先求出点C的横坐标,再通过证明四边形ABCD是平行四边形,求出AD的长即可得出点D的坐标.
(2)本题需先根据题意求出BO的长,即可得出点B的坐标,然后把点B的坐标代入二次函数的解析式求出a的值,即可得出结果.
点评:本题主要考查了二次函数的综合应用,在解题时要能把二次函数的图象和性质与平行四边形及菱形的性质相结合是本题的关键.
∴点C的横坐标为-4.
∴BC=4.
∵BC∥AD,CD∥AB,
∴四边形ABCD是平行四边形.
∴AD=4.
∴点D的坐标为(-6,0).
(2)能.
要使AC与BD互相垂直,必须使平行四边形ABCD是菱形,
即AB=BC=4.
∵AO=2,∴
 ,即点B的坐标为(0,
,即点B的坐标为(0, ).
).设所求的二次函数的解析式为y=a(x+2)2.
代入点B的坐标,得
 .
.∴
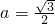 .
.∴当二次函数的解析式为
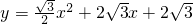 时,AC⊥BD.
时,AC⊥BD.分析:(1)本题需先求出点C的横坐标,再通过证明四边形ABCD是平行四边形,求出AD的长即可得出点D的坐标.
(2)本题需先根据题意求出BO的长,即可得出点B的坐标,然后把点B的坐标代入二次函数的解析式求出a的值,即可得出结果.
点评:本题主要考查了二次函数的综合应用,在解题时要能把二次函数的图象和性质与平行四边形及菱形的性质相结合是本题的关键.

练习册系列答案
相关题目