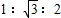题目内容
6、正三角形内切圆半径与外接圆半径及此正三角形高线之比为
1:2:3
.分析:先作出图形,根据等边三角形的性质确定它的内切圆和外接圆的圆心;通过特殊角进行计算,用内切圆半径来表示外接圆半径及此正三角形高线,最后写出比值.
解答:解:如图, △ABC是等边三角形,AD是高.
△ABC是等边三角形,AD是高.
点O是其外接圆的圆心,
由等边三角形的三线合一得点O在AD上,并且点O还是它的内切圆的圆心.
∵AD⊥BC,∠1=∠4=30°,
∴BD=2OD,而OA=OB,
∴AD=3OD,
∴OD:OA:AD=1:2:3.故填1:2:3.
 △ABC是等边三角形,AD是高.
△ABC是等边三角形,AD是高.点O是其外接圆的圆心,
由等边三角形的三线合一得点O在AD上,并且点O还是它的内切圆的圆心.
∵AD⊥BC,∠1=∠4=30°,
∴BD=2OD,而OA=OB,
∴AD=3OD,
∴OD:OA:AD=1:2:3.故填1:2:3.
点评:熟练掌握等边三角形的性质,特别是它的内切圆和外接圆是同心圆,并且圆心是它的高的三等分点,是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目