题目内容
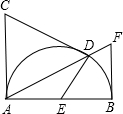如图，AB是半圆的直径，AC⊥AB，AC=AB，在半圆上任取一点D，过点D作DE⊥CD，交直径AB于点E，BF⊥AB，交线段AD的延长线于点F，问图中除了AB=AC外，是否还有其他两条线段相等？如果有，指出这两条相等的线段，并给出证明；如果没有，也要说明理由．
分析：先连接BD，由于AB是直径，那么BD⊥AD，又AB⊥BF，那么△BDF∽△ADB，利用相似三角形的性质可得，
=
，在△BDE和△ADC中，易证∠DBE=∠DAC，∠BDE=∠ADC，利用相似三角形的判定可得△BDE∽△ADC，于是BE：AC=BD：AD，等量代换有BF：AB=BE：AC，而AB=AC，那么BE=BF．
| BF |
| AB |
| BD |
| AD |
解答：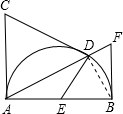
解：有，BE=BF．
连接BD，
∵AB是直径，
∴BD⊥AD，
又∵BF⊥AB，
∴△BDF∽△ADB，
∴
=
，
在△BDE和△ADC中，∠DBE=∠DAC，∠BDE=∠ADC，
∴△BDE∽△ADC，
∴BE：AC=BD：AD，
∴BF：AB=BE：AC，
又∵AB=AC，
∴BE=BF．
解：有，BE=BF．连接BD，
∵AB是直径，
∴BD⊥AD，
又∵BF⊥AB，
∴△BDF∽△ADB，
∴
| BF |
| AB |
| BD |
| AD |
在△BDE和△ADC中，∠DBE=∠DAC，∠BDE=∠ADC，
∴△BDE∽△ADC，
∴BE：AC=BD：AD，
∴BF：AB=BE：AC，
又∵AB=AC，
∴BE=BF．
点评：本题考查了相似三角形的判定和性质、圆中直径所对的圆周角等于90°、等角的余角相等、直角三角形斜边上的高所分成的两个三角形与原三角形相似．
练习册系列答案
相关题目
道BC的长86.96米，跑道的宽为l米．（π=3.14，结果精确到0.01）
